题目内容
16.已知点O(0,0),A(-8,0),B(0,3),Q(3,2),动点P满足条件|PA|=3|PO|.(1)求动点P的轨迹C的方程;
(2)设直线l经过点B,直线m经过点Q.问是否存在直线l使之被轨迹C截得的线段MN恰被直线m垂直平分?若存在,求出直线l与直线m的方程;若不存在,请说明理由.
分析 (1)设出点的坐标,利用动点P满足|PA|=3|PO|,建立方程,化简可得点P的轨迹方程.
(2)利用垂径定理,即可得出结论.
解答 解:(1)设P(x,y),则
∵点O(0,0),A(-8,0),动点P满足|PA|=3|PO|,
∴$\sqrt{(x+8)^{2}+{y}^{2}}$=3$\sqrt{{x}^{2}+{y}^{2}}$,
化简整理可得x2+y2-8x-32=0;
(2)x2+y2-8x-32=0可化为(x-4)2+y2=48,
由题意,m过圆心(4,0),∵直线m经过点Q(3,2),∴直线m的方程为y=$\frac{2}{3-4}$(x-4),即2x+y-8=0.
此时,直线l的斜率为$\frac{1}{2}$,直线l经过点B(0,3),∴直线l的方程为y=$\frac{1}{2}$x+3.
点评 本题考查轨迹方程,考查直线方程,考查学生的计算能力,正确运用两点间的距离公式是关键.

练习册系列答案
相关题目
8.若关于x的方程4x+(a-3)•2x+a=0在x∈(-∞,1)上有两个不等实根,则实数a 的取值范围是( )
| A. | (-∞,1)∪(9,+∞) | B. | ($\frac{2}{3}$,1) | C. | ($\frac{2}{3}$,3) | D. | (-1,3) |
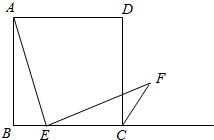 如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F设BE=x,记f(x)=$\overrightarrow{EC}$•$\overrightarrow{CF}$,则函数f(x)的值域是(0,4],当△ECF面积最大时,|$\overrightarrow{EF}$|=2$\sqrt{5}$.
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F设BE=x,记f(x)=$\overrightarrow{EC}$•$\overrightarrow{CF}$,则函数f(x)的值域是(0,4],当△ECF面积最大时,|$\overrightarrow{EF}$|=2$\sqrt{5}$.