题目内容
正数a,b,c满足:a2+ab+ac+bc=6+2
,则3a+b+2c的最小值是 .
| 5 |
考点:二维形式的柯西不等式
专题:综合题,不等式
分析:a2+ab+bc+ac=a(a+b)+c(a+b)=(a+b)(a+c)=6+2
,利用(a+b)(2a+2c)≤
[(a+b)+(2a+2c)]2=
(3a+b+2c)2,即可求得结论.
| 5 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:a2+ab+bc+ac=a(a+b)+c(a+b)=(a+b)(a+c)=6+2
,
∴(a+b)(2a+2c)=12+4
=(
+
)2,
∴(a+b)(2a+2c)≤
[(a+b)+(2a+2c)]2=
(3a+b+2c)2;
∴(
+
)2≤(3a+b+2c)2,
∴3a+b+2c的最小值为2
+2
.
故答案为:2
+2
.
| 5 |
∴(a+b)(2a+2c)=12+4
| 5 |
| 10 |
| 2 |
∴(a+b)(2a+2c)≤
| 1 |
| 4 |
| 1 |
| 4 |
∴(
| 10 |
| 2 |
∴3a+b+2c的最小值为2
| 10 |
| 2 |
故答案为:2
| 10 |
| 2 |
点评:本题考查柯西不等式,考查最小值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
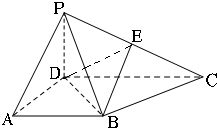 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E为PC的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E为PC的中点.