题目内容

若α与β的终边互为反向延长线，则有（　　）
A、α=β+180°
B、α=β-180°
C、α=-β
D、α=β+（2k+1）180°，k∈Z
考点：终边相同的角
专题：三角函数的图像与性质
分析：角α，β的终边互为反向延长线，则α与β的角的度数的差是π的整数倍，写出结果即可．
解答： 解：角α，β的终边互为反向延长线，则α与β的角的度数的差是π的整数倍，所以α=（2k+1）180°+β（k∈Z），
故选：D．
点评：利用角的终边的关系是平角，推出结果是解题的关键，考查理解能力，表达能力．
练习册系列答案
相关题目
执行如图所示的程序框图，则输出的a的值为（　　）（注：“a=2”，即为“a←2”或为“a：=2”．）
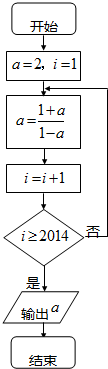
A、2
B、
1
3
C、-
1
2
D、-3
函数f（x）=8+2x-x2的单调递增区间是（　　）
A、[1，+∞）
B、（-∞，1]
C、[0，1]
D、（-∞，+∞
∫
π
2
-
π
2
xcosxdx的值为（　　）
A、0B、πC、2D、-2
设a=sin（sin210°），b=sin（cos210°），c=cos（cos210°），d=cos（sin210°），则a、b、c、d中最大的是（　　）
A、aB、bC、cD、d
等差数列{an}的各项均为正数，a1=3，前n项和为Sn，{bn}为等比数列，b1=1，且b2S2=64，b3S3=960．
（1）求an与bn；
（2）求{
1
Sn
}的前n项和．
已知向量
a
=（2，2），向量
b
与向量
c
的夹角为
3
4
π，且
a
•
b
=-2，
（1）求向量
b
；
（2）若
t
=（-1，0）且
b
⊥
t
，
c
=（cosA，2cos2
C
2
），其中A，C是△ABC的内角，∠B=60°，试求|
b
+
c
|的取值范围．
求证：函数f（x）=x3-x2在（
2
3
，+∞）上为增函数．
设An={
1
2
，
3
4
，
5
8
，…，
2n-1
2n
}（n∈N*，n≥2），An的所有非空子集中的最小元素的和为S，则S=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网