题目内容
下列函数中,既是奇函数又在区间(0,+∞)上单调递减的是( )
| A、y=-x2+2 | ||
B、y=
| ||
| C、y=2-x | ||
| D、y=lnx |
考点:函数单调性的判断与证明,函数奇偶性的性质
专题:函数的性质及应用
分析:根据基本初等函数的单调性与奇偶性,对选项中的函数判断即可.
解答:
解:对于A,y=-x2+2,是定义域上的偶函数,∴不满足条件;
对于B,y=
,是定义域上的奇函数,且在(0,+∞)上是单调减函数,满足条件;
对于C,y=2-x=(
)x,在定义域R上是非奇非偶的函数,∴不满足条件;
对于D,y=lnx,在定义域(0,+∞)上是非奇非偶的函数,∴不满足条件.
故选:B.
对于B,y=
| 1 |
| x |
对于C,y=2-x=(
| 1 |
| 2 |
对于D,y=lnx,在定义域(0,+∞)上是非奇非偶的函数,∴不满足条件.
故选:B.
点评:本题考查了基本初等函数的奇偶性与单调性的判断问题,是基础题目.

练习册系列答案
相关题目
《中国好歌曲》的五位评委刘欢、杨坤、周华健、蔡健雅、羽•泉组合给一位歌手给出的评分分别是:x1=18,x2=19,x3=20,x4=21,x5=22,现将这五个数据依次输入下面程序框进行计算,则输出的S值及其统计意义分别是( )


| A、S=2,即5个数据的方差为2 |
| B、S=2,即5个数据的标准差为2 |
| C、S=10,即5个数据的方差为10 |
| D、S=10,即5个数据的标准差为10 |
某几何体的三视图如图所示,则该几何体的体积为( )
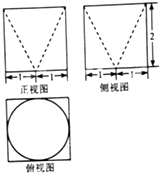

A、
| ||
B、
| ||
C、8-
| ||
D、8-
|
设m,n是正整数,多项式(1-2x)m+(1-5x)n中含x一次项的系数为-16,则含x2项的系数是( )
| A、-13 | B、6 | C、79 | D、37 |
七名同学站成一排照毕业纪念照,其中甲必须站在正中间,并且乙,丙两位同学要站在一起,则不同的排法有( )
| A、240种 | B、192种 |
| C、120种 | D、96种 |