题目内容
已知偶函数f(x)定义域为R,且在(-∞,0)上是减函数,又A,B是锐角三角形的两个内角,则( )
| A、f(sinA)>f(sinB) |
| B、f(cosA)<f(cosB) |
| C、f(sinA)<f(cosB) |
| D、f(sinA)>f(cosB) |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:根据函数奇偶性和单调性之间的关系即可得到结论.
解答:
解:∵A,B是锐角三角形的两个内角,
∴C=π-(A+B)<
,即A+B>
,
则0<
-B<A<
,
则sin(
-B)<sinA,即0<cosB<sinA,
∵偶函数f(x)定义域为R,且在(-∞,0)上是减函数,
∴f(sinA)>f(cosB),
故选:D
∴C=π-(A+B)<
| π |
| 2 |
| π |
| 2 |
则0<
| π |
| 2 |
| π |
| 2 |
则sin(
| π |
| 2 |
∵偶函数f(x)定义域为R,且在(-∞,0)上是减函数,
∴f(sinA)>f(cosB),
故选:D
点评:本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
给出下列四个命题:①?x∈R,x是方程3x-5=0的根; ②?x∈R,|x|>0; ③?x∈R;x2≤0,④?x∈R,都不是方程x2-3x+3=0的根.其中真命题的序号是( )
| A、①④ | B、①③ |
| C、①③④ | D、②③④ |
下列四个命题,其中正确的命题是( )
| A、命题“若a<b,则am2<bm2” | ||
| B、“a≤2”是“对任意的实数x,|x+1|+|x-1|≥a成立”的充分不必要条件 | ||
C、设随机变量ξ服从N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=
| ||
| D、命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x<0” |
若函数f(x)的定义域为R,那么“?x0∈R,f(-x0)=-f(x0)”是“f(x)为奇函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
曲线f(x)=ax3-3x+b在点(2,f(2))处的切线恰好是x轴,则a=( )
A、
| ||
B、
| ||
| C、1 | ||
| D、无法确定 |
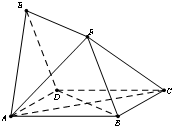 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60,且FA=FC.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60,且FA=FC.