题目内容
已知函数f(x)=
,x∈[1,+∞).
(1)当a=4时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
| x2+2x+a |
| x |
(1)当a=4时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
考点:函数恒成立问题,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)将a=4代入f(x),利用基本不等式求出最值,(2)将恒成立问题转化为最值问题求解,
解答:
解:(1)当a=4时,
f(x)=
=x+
+2≥2
+2=6,(当且仅当x=2时取得相等),
即函数最小值为6;
(2)f(x)>0即x+
+2>0对任意x∈[1,+∞),恒成立,
即a>-x(x+2)
a>-(x+1)2+1,
令g(x)=-(x+1)2+1,
g(x)的最大值为当x=1时取得,为g(1)=-3
所以有a>-3.
f(x)=
| x2+2x+4 |
| x |
| 4 |
| x |
x×
|
即函数最小值为6;
(2)f(x)>0即x+
| a |
| x |
即a>-x(x+2)
a>-(x+1)2+1,
令g(x)=-(x+1)2+1,
g(x)的最大值为当x=1时取得,为g(1)=-3
所以有a>-3.
点评:本题考查函数最值问题,用到了基本不等式和恒成立问题的转化求解,属于较经典的题型.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
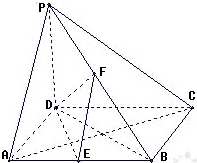 已知四棱锥P-ABCD,底面是边长为a的正方形,PD⊥底面ABCD,PD=DC,E、F分别是AB、PB的中点,
已知四棱锥P-ABCD,底面是边长为a的正方形,PD⊥底面ABCD,PD=DC,E、F分别是AB、PB的中点,