题目内容
8. 已知正四棱锥P-ABCD,底面正方形的边长是2,高与斜高的夹角为30°,那么正四棱锥的侧面积为8.
已知正四棱锥P-ABCD,底面正方形的边长是2,高与斜高的夹角为30°,那么正四棱锥的侧面积为8.
分析 利用已知中,正四棱锥底面正方形的边长为2,高与斜高的夹角为30°,求出正四棱锥的高PO,斜高PE,底面边心距OE组成直角△POE,求出斜高和高,代入棱锥的侧面积和表面积公式,即可求得答案.
解答 解:如图,正四棱锥的高PO,斜高PE,底面边心距OE组成直角△POE.
∵OE=1,∠OPE=30°,
∴斜高PE=2,
∴S正棱锥侧=$\frac{1}{2}$Ch′=$\frac{1}{2}$×4×2×2=8,
故答案为8.
点评 本题考查的知识点是棱锥的侧面积,主要通过正棱锥的高、斜高、底面边心距组成的直角三角形寻找到各量的关系,并求解.

练习册系列答案
相关题目
18.f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)-f(x)≤0.对任意正数a,b,若a<b,则必有( )
| A. | bf(a)≤af(b) | B. | af(b)≤bf(a) | C. | bf(a)≤f(a) | D. | af(a)≤f(b) |
18.某高校“统计初步”课程的教师为了判断主修统计专业是否与性别有关,随机调查了该选修课的一些学生情况.23名男生中,有10人是统计专业;27名女生中,有20人是统计专业.
(1)根据统计数据填写下面的2×2列联表.
(2)如果判断主修统计专业与性别有关,那么这种判断出错的概率最大不超过多少?
附表:
公式:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
(1)根据统计数据填写下面的2×2列联表.
| 非统计专业 | 统计专业 | 总计 | |
| 男 | |||
| 女 | |||
| 总计 |
附表:
| P(k2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
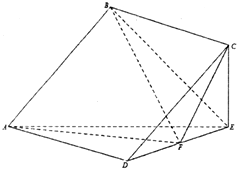 在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.
在几何体ABCDE中,四边形ABCD是正方形,CE⊥平面ADE且CE=EF=2,F是线段DE的中点.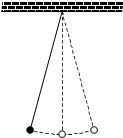 如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.
如图,单摆的摆线离开平衡位置的位移S(厘米)和时间t(秒)的函数关系是S=$\frac{1}{2}$sin(2t+$\frac{π}{3}$),则摆球往复摆动一次所需要的时间是π秒.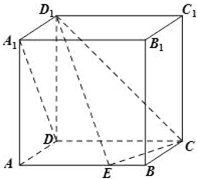 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
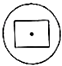
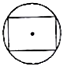
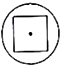
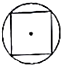
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.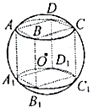 如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )
如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )