题目内容
3.求函数f(x)=x3-3x2-9x+2的单调区间和极值.分析 由f(x)求得f′(x)通过对f'(x)>0与f'(x)<0的分析,可求得f(x)的单调区间和极值.
解答 解:函数f(x)=x3-3x2-9x+2,可得:f'(x)=3x2-6x-9
令 f'(x)=0,解得x1=-1,x2=3.
列表讨论f(x)、f'(x)的变化情况:
| x | (-∞,-1) | -1 | (-1,3) | 3 | (3,+∞) |
| f'(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值7 | ↘ | 极小值-1 | ↗ |
当x=-1时,f(x)的极大值是f(-1)=7;
当x=3时,f(x)的极小值是f(3)=-25.
点评 本题考查利用导数研究函数的单调性与极值,着重考查导数与单调性间的关系及应用,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
13.要得到y=sin2x的图象,只需将y=sin(2x-$\frac{π}{4}$)的图象是( )
| A. | 向右平移$\frac{π}{8}$ | B. | 向左平移$\frac{π}{8}$ | C. | 向右平移$\frac{π}{4}$ | D. | 向左平移$\frac{π}{4}$ |
18.f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)-f(x)≤0.对任意正数a,b,若a<b,则必有( )
| A. | bf(a)≤af(b) | B. | af(b)≤bf(a) | C. | bf(a)≤f(a) | D. | af(a)≤f(b) |
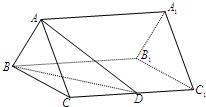 如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°.
如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D是侧棱CC1的中点,直线AD与侧BB1C1C所成的角为45°. 如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.
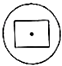
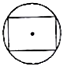
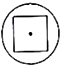
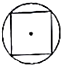
如图,四棱锥P-ABCD中,PB⊥底面ABCD.底面ABCD为直角梯形,∠ABC=90°,AD∥BC,BC=2,AB=AD=PB=1,点E为棱PA的中点.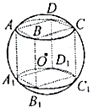 如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )
如图所示,几何体为一个球挖去一个内接正方体得到的组合体,现用一个经过球心的平面截它,所得的截面图形不可能是( )