题目内容
10.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点作圆x2+y2=a2的两条切线,切点分别为A,B,若∠AOB=120°(O是坐标原点),则双曲线C的离心率为( )| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
分析 根据题意可先求得∠AOF利用OF和OA,在直角三角形中求得的$\frac{a}{c}$值,进而可求得双曲线的离心率
解答 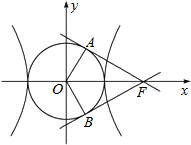 解:如图,由题知OA⊥AF,OB⊥BF且∠AOB=120°,
解:如图,由题知OA⊥AF,OB⊥BF且∠AOB=120°,
∴∠AOF=60°,又OA=a,
OF=c,
∴$\frac{a}{c}$=$\frac{OA}{OF}$=cos60°=$\frac{1}{2}$,
∴e=$\frac{c}{a}$=2,
故选:A
点评 本题主要考查了双曲线的简单性质.解题的过程中采用了数形结合的思想,使问题的解决更直观.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.等差数列{an}的前n项和为Sn,若a1000+a1018=2,则S2017=( )
| A. | 1008 | B. | 1009 | C. | 2016 | D. | 2017 |
18.甲、乙两人在一座9层大楼的地层进入电梯,若每个人直第二层开始在第一层离开电梯是等可能的,则2个人在不同楼层离开的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{6}$ | C. | $\frac{8}{9}$ | D. | $\frac{7}{8}$ |
5.在面积为S的△ABC的边AB含任取一点P,则△PBC的面积大于$\frac{S}{4}$的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{2}{3}$ |
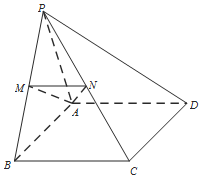 在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.
在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.