题目内容
已知不等式3x+b＞
（-2≤x≤2），求b的取值范围．
| 4-x2 |
考点：其他不等式的解法
专题：计算题,数形结合,函数的性质及应用,不等式的解法及应用
分析：不等式3x+b＞
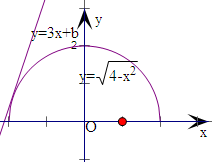
（-2≤x≤2）表示直线恒在半圆上方，在同一坐标系中，作出直线y=3x+b，半圆y=
，求出直线和半圆相切时，b的值，再向上平移，即可满足条件，求得b的范围．
| 4-x2 |
| 4-x2 |
解答：
解：令y=
，（-2≤x≤2）
则x2+y2=4，表示圆心为（0，0），半径为2的半圆，
在同一坐标系中，作出直线y=3x+b，半圆y=
，
由图可得，当直线和半圆相切时，恰有一个交点，
则由相切的条件可得d=
=2，
解得b=±2
．
当直线向上平移时，恒在半圆上方，满足条件．
则b的取值范围是b＞2
．
解：令y=| 4-x2 |
则x2+y2=4，表示圆心为（0，0），半径为2的半圆，
在同一坐标系中，作出直线y=3x+b，半圆y=
| 4-x2 |
由图可得，当直线和半圆相切时，恰有一个交点，
则由相切的条件可得d=
| |b| | ||
|
解得b=±2
| 10 |
当直线向上平移时，恒在半圆上方，满足条件．
则b的取值范围是b＞2
| 10 |
点评：本题考查不等式表示的几何意义，考查直线和圆的位置关系，考查点到直线的距离公式的运用，考查数形结合的思想方法，考查运算能力，属于中档题．
练习册系列答案
小学期末标准试卷系列答案
相关题目
在正四棱柱ABCD-A′B′C′D′中，AB=1，A′A=2，则 A′C与BC所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
球O的一个截面圆的圆心为M，圆M的半径为
，OM的长度为球O的半径的一半，则球O的表面积为（ ）
| 3 |
| A、4π | ||
B、
| ||
| C、12π | ||
| D、16π |
图中的程序框图所描述的算法称为欧几里得辗转相除法． 若输入m=209，n=121，则输出m=已知数列{an}是公比为2的等比数列，若a3a4a5=8，则a6等于（ ）
| A、4 | B、8 | C、12 | D、16 |
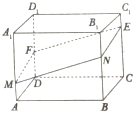如图4所示，已知直四棱柱ABCD-A1B1C1D1的底面是棱形，其边长为4，∠BAD=60°，点M，N，E分别在棱AA1，BB1，CC1上，过M，N，E的面与棱DD1交于F，AM=2，BN=4，CE=5．求：已知函数定义域（-1，1]，满足f（x）+1=
，当x∈[0，1]时，f（x）=x，若函数g（x）=
，方程g（x）-mx-2m=0有三个实根，则实数m的取值范围是（ ）
| 1 |
| f(x+1) |
|
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|