题目内容
在正四棱柱ABCD-A′B′C′D′中，AB=1，A′A=2，则 A′C与BC所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：空间中直线与直线之间的位置关系
专题：空间角
分析：连结A′B，结合几何体的特征，直接求解 A′C与BC所成角的余弦值即可．
解答：
解：如图：正四棱柱ABCD-A′B′C′D′中，AB=1，A′A=2，
连结A′B，则 A′C与BC所成角就是直角三角形A′BC中的∠A′CB，
A′C与BC所成角的余弦值为：
=
=
．
故选：C．
解：如图：正四棱柱ABCD-A′B′C′D′中，AB=1，A′A=2，连结A′B，则 A′C与BC所成角就是直角三角形A′BC中的∠A′CB，
A′C与BC所成角的余弦值为：
| BC |
| A′C |
| 1 | ||
|
| ||
| 6 |
故选：C．
点评：本题考查几何体的特征，直线与直线所成角的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
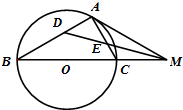已知Rt△ABC（∠A=90°）的外接圆为圆O，过A的切线AM交BC于点M，过M作直线交AB，AC于点D，E，且AD=AE
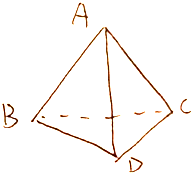如图三棱锥A-BCD中DC⊥BC，BC=2
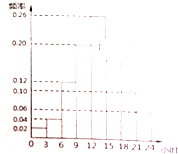天猫电器城对TCL官方旗舰店某款4K超高清电视机在2014年11月11日的销售情况进行了统计，如图所示，数据显示，该日TCL官方旗舰店在[0，3）小时销售了该款电视机2台．已知数列{an}中，有an+1=an+4，且a1+a4=14．
（1）求{an}的通项公式an与前n项和公式Sn；
（2）令bn=
，若{bn}是等差数列，求数列{
}的前n项和Tn．
（1）求{an}的通项公式an与前n项和公式Sn；
（2）令bn=
| Sn |
| n+k |
| 1 |
| bnbn+1 |
存在实数a使得方程cosx=a在[0，2π]上有两个不相等的实数根x1，x2，则sin
=（ ）
| x1+x2 |
| 3 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|