题目内容
3.已知一家公司生产某种产品的年固定成本为6万元,每生产1千件需另投入2.9万元.设该公司一年内生产该产品x千件并全部销售完,每千件的销售收入为g(x)万元,且g(x)=$\left\{\begin{array}{l}{8+\frac{{2}^{x}}{64x},1≤x≤8}\\{11-\frac{1}{30}{x}^{2},x>8}\end{array}\right.$.(1)写出年利润f(x)(万元)关于年产量x(千件)的函数解析式;
(2)求该公司生产这一产品的最大利润及相应的年产量.(年利润=年销售收入-年总成本)
分析 (1)通过讨论x的范围,分别求出f(x)的解析式即可;
(2)通过讨论x的范围,求出各个区间上的函数的单调性,求出函数的最大值即可.
解答 解:(1)当1≤x≤8时,f(x))=x(8+$\frac{{2}^{x}}{64x}$)-(6+2.9x)=$\frac{{2}^{x}}{64}$+5.1x-6,
当x>8时,f(x)=xg(x)-(6+2.9x)=8.1x-$\frac{{x}^{3}}{30}$-6,
∴f(x)=$\left\{\begin{array}{l}{\frac{{2}^{x}}{64}+5.1x-6,1≤x≤8}\\{8.1x-\frac{{x}^{3}}{30}-6,x>8}\end{array}\right.$;
(2)当1≤x≤8时,f(x)=$\frac{{2}^{x}}{64}$+5.1x-6为增函数,
此时,f(x)max=f(8)=4+5.1×8-6=38.8,
当x>8时,由f′(x)=8.1-$\frac{{x}^{2}}{10}$=0,解得:x=9,
x∈(8,9)时,f′(x)>0,f(x)递增,
x∈(9,+∞)时,f′(x)<0,f(x)递减,
此时,f(x)max=f(9)=8.1×9-$\frac{1}{30}$×93-6=42.6,
38.8<42.6,因此x=9时,f(x)取得最大值为42.6万元,
故当年产量为9千件时,该公式在这一产品的生产中获得最大年利润42.6万元.
点评 本题考查了求函数的解析式问题,考查函数的单调性、最值问题,是一道中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
14.已知a>b>1,0<c<1,则下列不等式正确的是( )
| A. | ac<bc | B. | ca>cb | C. | logac>logbc | D. | logca>logcb |
14.半径为R的球O中有两个半径分别为2$\sqrt{3}$与2$\sqrt{2}$的截面圆,它们所在的平面互相垂直,且两圆的公共弦长为R,则球O表面积为( )
| A. | 64π | B. | 100π | C. | 36π | D. | 24π |
 中,
中, ,过
,过 的中点
的中点 作平面
作平面 的垂线,交平面
的垂线,交平面 于
于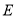 ,则
,则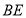 与平面
与平面 所成角的正切值为( )
所成角的正切值为( )
 B.
B. C.
C.  D.
D.
 的底面
的底面 是矩形,平面
是矩形,平面 平面
平面 ,
,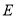 是
是 的中点,且
的中点,且 ,
, .
.
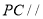 平面
平面 ;
; 的体积.
的体积.