题目内容
14.半径为R的球O中有两个半径分别为2$\sqrt{3}$与2$\sqrt{2}$的截面圆,它们所在的平面互相垂直,且两圆的公共弦长为R,则球O表面积为( )| A. | 64π | B. | 100π | C. | 36π | D. | 24π |
分析 设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,则OO1EO2为矩形,于是OO1=O2E=$\sqrt{{R}^{2}-8}$,
AB=2AE=2$\sqrt{12-{R}^{2}+8}$=R即可.
解答  解:设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,则OO1EO2为矩形,于是OO1=O2E=$\sqrt{{R}^{2}-8}$,
解:设两圆的圆心分别为O1、O2,球心为O,公共弦为AB,其中点为E,则OO1EO2为矩形,于是OO1=O2E=$\sqrt{{R}^{2}-8}$,
AB=2AE=2$\sqrt{12-{R}^{2}+8}$=R
∴R=4.则球O表面积为4πR2=64π
故选:A.
点评 本题主要考查球的有关概念以及两平面垂直的性质,是对基础知识的考查.解决本题的关键在于得到OO1EO2为矩形.属于中档题,

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.若集合M={y|y=2017x},S={x|y=log2017(x-1)},则下列结论正确的是( )
| A. | M=S | B. | M∩S=∅ | C. | M∪S=S | D. | M∪S=M |
19. 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )| A. | 70 | B. | 72 | C. | 74 | D. | 76 |
6.推理过程:“因为无理数是无限小数,$\frac{1}{3}$=0.333333333333…是无限小数,所以$\frac{1}{3}$是无理数”,以下说法正确的是( )
| A. | 完全归纳推理,结论正确 | B. | 三段论推理,结论正确 | ||
| C. | 传递性关系推理,结论正确 | D. | 大前提正确,推理的结论错误 |
 中,以
中,以 为极点,
为极点,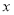 轴正半轴为极轴建立坐标系,曲线
轴正半轴为极轴建立坐标系,曲线 极坐标方程为
极坐标方程为 ,曲线
,曲线 参数方程为
参数方程为 (
( 为参数).
为参数). 的直角坐标方程;
的直角坐标方程; 与
与 有两个公共点时,求实数
有两个公共点时,求实数 取值范围.
取值范围.