题目内容
8.已知等差数列{an}中,a2=3,a5=6.(1)求数列{an}的通项公式
(2)设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$,求数列{bn}的前n项和Sn.
分析 (1)利用等差数列关系式求出公差,然后求解数列的通项公式.
(2)化简数列的通项公式,利用裂项消项法求解数列的和即可.
解答 解:等差数列{an}中,a2=3,a5=6.
可得d=$\frac{{a}_{5}-{a}_{2}}{5-2}$=$\frac{6-3}{5-2}$=1,a1=a2-d=2.
所以an=n+1.
(2)bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}$$-\frac{1}{n+2}$.
数列{bn}的前n项和Sn=$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n+1}-\frac{1}{n+2}$=$\frac{n}{2n+4}$.
点评 本题考查数列通项公式的求法,数列求和的方法:裂项消项法的应用,考查计算能力.

练习册系列答案
相关题目
19. 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )
某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示),估计该次考试的平均分$\overline{x}$(同一组中的数据用该组的区间中点值代表)为( )| A. | 70 | B. | 72 | C. | 74 | D. | 76 |
16.在如图的程序框图中,若输入的x值为2,则输出的y值为( )


| A. | 0 | B. | $\frac{1}{2}$ | C. | -1 | D. | -$\frac{3}{2}$ |
 如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3.
如图,在四棱锥E-ABCD中,EC⊥底面ABCD,AB⊥BC,AB∥CD,AB=1,CB=CD=CE=3. 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系, 已知点
轴的非负半轴为极轴建立极坐标系, 已知点 的极坐标为
的极坐标为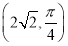 ,曲线
,曲线 的参数方程为
的参数方程为 为参数).
为参数). 过
过 与点
与点 轴对称, 求曲线
轴对称, 求曲线 的右焦点为
的右焦点为 ,直线
,直线 与双曲线
与双曲线 的渐近线在第一象限的交点为
的渐近线在第一象限的交点为 为坐标原点,若
为坐标原点,若 的面积为
的面积为 ,则双曲线
,则双曲线 B.
B. C.
C. D.
D.
 如图,在四边形ABCD中,∠DAB=$\frac{π}{3}$,AD:AB=2:3,BD=$\sqrt{7}$,AB⊥BC.
如图,在四边形ABCD中,∠DAB=$\frac{π}{3}$,AD:AB=2:3,BD=$\sqrt{7}$,AB⊥BC.