题目内容
已知集合A={x|x(x-1)(x-2)=0}的非空真子集的个数是( )
| A、5 | B、6 | C、7 | D、8 |
考点:子集与真子集
专题:集合
分析:通过解方程求出集合A,然后写出A的所有非空真子集即可得到集合A的非空真子集个数.
解答:
解:A={0,1,2},所以集合A的非空真子集为:
{0},{1},{2},{0,1},{0,2},{1,2};
∴A的非空真子集的个数是6.
故选B.
{0},{1},{2},{0,1},{0,2},{1,2};
∴A的非空真子集的个数是6.
故选B.
点评:考查描述法表示集合,将描述法表示集合转变成列举法表示,真子集的概念,这里要注意的是要找A的非空真子集,不包括空集.

练习册系列答案
相关题目
将甲、乙、丙、丁、戊5名大学生分配到3个乡镇去当村官,设事件A为“每个乡镇至少有一名大学生村官”,事件B为“甲、乙、丙三人在同一个乡镇当村官”,则概率P(B|A)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知loga(3a-1)恒为正数,则实数a的取值范围是( )
A、(-∞,
| ||||
B、(
| ||||
| C、(1,+∞) | ||||
D、(
|
设随机变量X~N(1,4),且P(X≤a)=P(X>2),则实数a的值为( )
| A、3 | B、2 | C、1 | D、0 |
函数f(x)=2x满足( )
| A、f(xy)=f(x)+f(y) |
| B、f(xy)=f(x)•f(y) |
| C、f(x+y)=f(x)+f(y) |
| D、f(x+y)=f(x)•f(y) |
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)<
,则f(x)<
+
的解集为( )
| 1 |
| 3 |
| x |
| 3 |
| 2 |
| 3 |
| A、{x|-1<x<1} |
| B、{x|<-1} |
| C、{x|x<-1或x>1} |
| D、{x|x>1} |
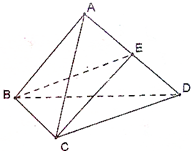 在四面体ABCD中,E为AD中点,△ABC与△BCD都是边长为4的正三角形.
在四面体ABCD中,E为AD中点,△ABC与△BCD都是边长为4的正三角形.