题目内容
函数y=
的图象与函数y=2sinπx,(-2≤x≤4)的图象所有交点的横坐标之和等于( )
| 1 |
| 1-x |
| A、8 | B、6 | C、4 | D、2 |
考点:数列与函数的综合,数列的求和
专题:函数的性质及应用,等差数列与等比数列
分析:函数y1=
与y2=2sinπx的图象有公共的对称中心(1,0),作出两个函数的图象,利用数形结合思想能求出结果.
| 1 |
| 1-x |
解答:
解:函数y1=
,
y2=2sinπx的图象有公共的对称中心(1,0),
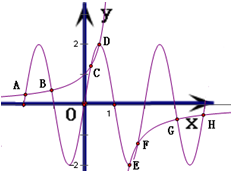
作出两个函数的图象,如图,
当1<x≤4时,y1<0
而函数y2在(1,4)上出现1.5个周期的图象,
在(1,
)和(
,
)上是减函数;
在(
,
)和(
,4)上是增函数.
∴函数y1在(1,4)上函数值为负数,
且与y2的图象有四个交点E、F、G、H
相应地,y1在(-2,1)上函数值为正数,
且与y2的图象有四个交点A、B、C、D
且:xA+xH=xB+xG=xC+xF=xD+xE=2,
故所求的横坐标之和为8.
故选:A.
| 1 |
| 1-x |

y2=2sinπx的图象有公共的对称中心(1,0),
作出两个函数的图象,如图,
当1<x≤4时,y1<0
而函数y2在(1,4)上出现1.5个周期的图象,
在(1,
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
在(
| 3 |
| 2 |
| 5 |
| 2 |
| 7 |
| 2 |
∴函数y1在(1,4)上函数值为负数,
且与y2的图象有四个交点E、F、G、H
相应地,y1在(-2,1)上函数值为正数,
且与y2的图象有四个交点A、B、C、D
且:xA+xH=xB+xG=xC+xF=xD+xE=2,
故所求的横坐标之和为8.
故选:A.
点评:本题考查两个函数的图象的交点的横坐标之和的求法,是基础题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
A是直二面角α-l-β的棱l上的一点,两条长为a的线段AB、AC分别在α、β内,且分别与l成45°角,则BC的长为( )
| A、a | ||||
B、a或
| ||||
C、
| ||||
D、a或
|
 如图所示:在四棱锥中A-BCDE中,AE⊥面EBCD,且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点(不包括端点),当F时BC的中点时,求点F到面ACD的距离.
如图所示:在四棱锥中A-BCDE中,AE⊥面EBCD,且四边形EBCD是菱形,∠BED=120°,AE=BE=2,F是BC上的动点(不包括端点),当F时BC的中点时,求点F到面ACD的距离. 已知函数f(x)=|3x-6|-|x-4|
已知函数f(x)=|3x-6|-|x-4|