题目内容
某同学在研究函数f（x）=| x2+1 |
| x2-6x+10 |
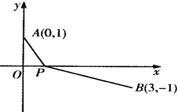
| (x-0)2+(0-1)2 |
| (x-3)2+(0+1)2 |
①f（x）的图象是中心对称图形；
②f（x）的图象是轴对称图形；
③函数f（x）的值域为[
| 13 |
④函数f（x）在区间（-∞，3）上单调递减；
⑤方程f[f(x)]=1+
| 10 |
上述关于函数f（x）的描述正确的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
考点：两点间距离公式的应用
专题：函数的性质及应用
分析：由函数的几何意义可得函数的值域及单调性，结合函数的值域和单调性逐个选项验证即可作出判断．
解答：
解：∵函数f（x）的最小值为|AB|=
=
，
∴函数的值域[
，+∞)，显然③正确；
由函数的值域知，函数图象不可能为中心对称图形，故①错误；
又∵直线AB与x轴交点的横坐标为
，显然有f(
-x)=f(
+x)，
∴函数的图象关于直线x=
对称，故②正确；
由函数的几何意义知函数在区间(-∞，
]上单调递减，在区间[
，+∞)上单调递增，故④错误；
令t=f（x），由f(t)=1+
得t=0或t=3，由函数的值域可知不成立，∴方程无解，故⑤错误，
故选：B．
| 32+(1+1)2 |
| 13 |
∴函数的值域[
| 13 |
由函数的值域知，函数图象不可能为中心对称图形，故①错误；
又∵直线AB与x轴交点的横坐标为
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
∴函数的图象关于直线x=
| 3 |
| 2 |
由函数的几何意义知函数在区间(-∞，
| 3 |
| 2 |
| 3 |
| 2 |
令t=f（x），由f(t)=1+
| 10 |
故选：B．
点评：本题考查函数的性质，涉及两点间的距离公式，属中档题．
练习册系列答案
相关题目
直线y=kx-2交抛物线y2=8x于A、B两点，若弦AB的中点M（2，m），则k=（ ）
| A、2或-1 | B、-1 | C、2 | D、3 |
命题p：幂函数y=x
在（-∞，0）上单调递减；命题q：已知函数f（x）=x3-3x2+m，若a，b，c∈[1，3]，且f（a），f（b），f（c）能构成一个三角形的三边长，且4＜m＜8，则（ ）
| 2 |
| 3 |
| A、p且q为真命题 |
| B、p或q为假命题 |
| C、（￢p）且q为真命题 |
| D、p且（￢q）为真命题 |