题目内容
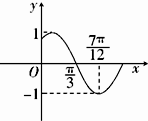
20. 已知函数y=2sin(ωx+φ)(ω>0)的部分图象如图所示,点A(-$\frac{π}{6}$,0)、B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则($\overrightarrow{AD}$-$\overrightarrow{EA}$)•(ω$\overrightarrow{AC}$)的值是( )
已知函数y=2sin(ωx+φ)(ω>0)的部分图象如图所示,点A(-$\frac{π}{6}$,0)、B、C是该图象与x轴的交点,过点B作直线交该图象于D、E两点,点F($\frac{7π}{12}$,0)是f(x)的图象的最高点在x轴上的射影,则($\overrightarrow{AD}$-$\overrightarrow{EA}$)•(ω$\overrightarrow{AC}$)的值是( )| A. | 2π2 | B. | π2 | ||
| C. | 2 | D. | 以上答案均不正确 |
分析 根据函数y=2sin(ωx+φ)(ω>0)的部分图象,利用周期性求得ω,可得C、B的坐标,再根据线段EF关于点B对称,利用两个向量的加减法及其几何意义求得要求式子的值.
解答 解:根据函数y=2sin(ωx+φ)(ω>0)的部分图象可得$\frac{3}{4}$•$\frac{2π}{ω}$=$\frac{7π}{12}$-(-$\frac{π}{6}$),∴ω=2.
∵2•(-$\frac{π}{6}$)+φ=π,∴φ=$\frac{4π}{3}$,函数y=2sin(2x+$\frac{4π}{3}$),可得C($\frac{5π}{6}$,0),
故AC的中点B($\frac{π}{3}$,0).
由题意可得线段EF关于点B对称,则($\overrightarrow{AD}$-$\overrightarrow{EA}$)•(ω$\overrightarrow{AC}$)=($\overrightarrow{AD}$+$\overrightarrow{AE}$)•(ω$\overrightarrow{AC}$)
=2$\overrightarrow{AB}$•2$\overrightarrow{AC}$=4|AB|•|AC|=4•$\frac{T}{2}$•T=2T2=2•${(\frac{2π}{2})}^{2}$=2π2,
故选:A.
点评 本题主要考查正弦函数的图象,两个向量的加减法及其几何意义,属于中档题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
11.集合A={1,2,3,4},B={x∈R|x≤3},则A∩B=( )
| A. | {1,2,3,4} | B. | {1,2,3} | C. | {2,3} | D. | {1,4} |
 如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.
如图,矩形ORTM内放置6个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则$(\overrightarrow{AE}-\overrightarrow{BC})•\overrightarrow{BD}$=-6.