题目内容
15．已知函数y=sin（ωx+φ）的图象如图所示，则ω=2，φ=$\frac{π}{3}$．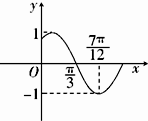
分析 由周期求出ω，由五点法作图求出φ的值，可得函数的解析式．
解答 解：根据函数y=sin（ωx+φ）的图象，可得$\frac{1}{4}•\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$，∴ω=2，
再根据五点法作图可得2•$\frac{π}{3}$+φ=π，求得φ=$\frac{π}{3}$，
故答案为：2；$\frac{π}{3}$．
点评 本题主要考查利用y=Asin（ωx+φ）的图象特征，由函数y=Asin（ωx+φ）的部分图象求解析式，由周期求出ω，由五点法作图求出φ的值，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知函数y=2sin（ωx+φ）（ω＞0）的部分图象如图所示，点A（-$\frac{π}{6}$，0）、B、C是该图象与x轴的交点，过点B作直线交该图象于D、E两点，点F（$\frac{7π}{12}$，0）是f（x）的图象的最高点在x轴上的射影，则（$\overrightarrow{AD}$-$\overrightarrow{EA}$）•（ω$\overrightarrow{AC}$）的值是（ ）
10．设函数f（x）=2${\;}^{\sqrt{|x|+1}}$-$\frac{3}{1+{x}^{2}}$，则使得f（x2+$\frac{2}{3}$x+2）＞f（-x2+x-1）成立的x的取值范围是（ ）
| A． | [-$\frac{3}{5}$，+∞） | B． | （-∞，$\frac{3}{5}$] | C． | （-$\frac{3}{5}$，+∞） | D． | $（{-\frac{3}{5}，\frac{3}{5}}）$ |
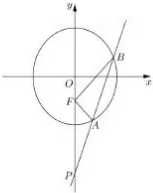如图，设F是椭圆$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的下焦点，直线y=kx-4（k＞0）与椭圆相交于A、B两点，与y轴交于点P