题目内容
7．已知向量$\overrightarrow a=（2x，1，3）$，向量$\overrightarrow b=（1，-2y，9）$，若$\overrightarrow a$与$\overrightarrow b$共线，则x=-$\frac{1}{6}$，y=-$\frac{3}{2}$．分析 利用向量共线定理即可得出．
解答 解：∵$\overrightarrow a$与$\overrightarrow b$共线，
∴存在实数λ使得：$\overrightarrow b$=λ$\overrightarrow a$，
∴$\left\{\begin{array}{l}{\stackrel{1=2xλ}{-2y=λ}}\\{9=3λ}\end{array}\right.$，解得x=-$\frac{1}{6}$，y=-$\frac{3}{2}$．
故答案为：-$\frac{1}{6}$，-$\frac{3}{2}$．
点评 本题考查了向量共线定理的应用，考查了计算能力，属于基础题．
练习册系列答案
相关题目
17．
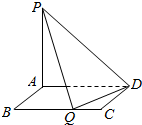如图所示，矩形ABCD的边AB=m，BC=4，PA⊥平面ABCD，PA=3，现有数据：
①$m=\frac{3}{2}$；②m=3；③m=4；④$m=\sqrt{5}$．若在BC边上存在点Q（Q不在端点B、C处），使PQ⊥QD，则m可以取（ ）
如图所示，矩形ABCD的边AB=m，BC=4，PA⊥平面ABCD，PA=3，现有数据：①$m=\frac{3}{2}$；②m=3；③m=4；④$m=\sqrt{5}$．若在BC边上存在点Q（Q不在端点B、C处），使PQ⊥QD，则m可以取（ ）
| A． | ①② | B． | ①②③ | C． | ②④ | D． | ① |
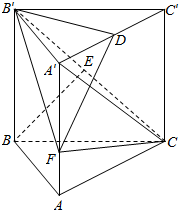如图，在直三棱柱ABC-A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2，BB1=3，D为A1C1的中点，E为B1C的中点．
19．已知一个空间几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积是（ ）
| A． | 2 | B． | 4 | C． | 6 | D． | 12 |