题目内容
在△ABC中，若AB=2，AC=3，∠A=60°，则BC的长为（ ）
A、
| ||
B、
| ||
| C、3 | ||
D、
|
考点：余弦定理
专题：三角函数的求值
分析：由AB，AC，以及cosA的值，利用余弦定理即可求出BC的长．
解答：
解：∵在△ABC中，AB=2，AC=3，∠A=60°，
∴由余弦定理得：BC2=AB2+AC2-2AB•ACcosA=4+9-6=7，
则BC=
．
故选：D．
∴由余弦定理得：BC2=AB2+AC2-2AB•ACcosA=4+9-6=7，
则BC=
| 7 |
故选：D．
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
一线名师提优试卷系列答案
相关题目
如图，在三棱锥P-ABC中，△PAB和△CAB都是以AB为斜边的等腰直角三角形，D、E、F分别是PC、AC、BC的中点．
（文科）如图，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=已知方程
=k在（0，+∞）上有两个不同的解α，β（α＜β），则下面结论正确的是（ ）
| |sinx| |
| x |
| A、sinα=αcosβ |
| B、sinα=-αcosβ |
| C、cosα=βsinβ |
| D、sinβ=-βsinα |
有一个几何体的三视图如图所示，这个几何体是一个（ ）
| A、棱台 | B、棱锥 | C、棱柱 | D、圆柱 |
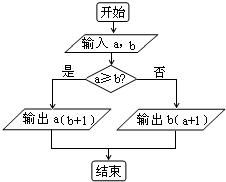
对于实数a和b，定义运算a*b，运算原理如图所示，则式子(
)-2*lne2的值为（ ）
| 1 |
| 2 |
| A、8 | ||
| B、10 | ||
| C、12 | ||
D、
|
若0＜x＜y＜1，则（ ）
| A、logx3＜logy3 | ||||
| B、3y＜3x | ||||
| C、log4x＜log4y | ||||
D、（
|