题目内容
已知圆心为O的圆内有一条弦BC,其长为2,动点为A,在圆上运动,且∠BAC=45°,若∠ABC为锐角,则
•
的取值范围是 .
| OA |
| BC |
考点:平面向量数量积的运算
专题:计算题,三角函数的图像与性质,平面向量及应用
分析:首先建立恰当的直角坐标系,根据直角坐标系确定各点的坐标,进一步利用向量的数量积转化成利用定义域求三角函数的值域.
解答:
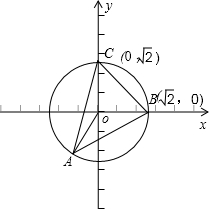 解:如图所示:|BC|=2,∠BOC=90°,∠CAB=45°,
解:如图所示:|BC|=2,∠BOC=90°,∠CAB=45°,
由于∠B为锐角,则:点A只能在左半圆上,
故设:A(
cosθ,
sinθ)(
<θ<
)
B(
,0),C(0,
),
=(
cosθ,
sinθ),
=(-
,
),
所以:
•
=-2cosθ+2sinθ=2
sin(θ-
)
由于
<θ<
,
所以:-
<sin(θ-
)≤1,
则:-2<
•
≤2
.
故答案为:(-2,2
].
 解:如图所示:|BC|=2,∠BOC=90°,∠CAB=45°,
解:如图所示:|BC|=2,∠BOC=90°,∠CAB=45°,由于∠B为锐角,则:点A只能在左半圆上,
故设:A(
| 2 |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
B(
| 2 |
| 2 |
| OA |
| 2 |
| 2 |
| BC |
| 2 |
| 2 |
所以:
| OA |
| BC |
| 2 |
| π |
| 4 |
由于
| π |
| 2 |
| 3π |
| 2 |
所以:-
| ||
| 2 |
| π |
| 4 |
则:-2<
| OA |
| BC |
| 2 |
故答案为:(-2,2
| 2 |
点评:本题考查的知识要点:向量的数量积,三角函数的恒等变换,利用正弦型函数的定义域求值域.

练习册系列答案
相关题目
若直线(3λ+1)x+(1-λ)y+6-6λ=0与不等式组
表示的平面区域有公共点,则实数λ的取值范围是( )
|
A、(-∞,-
| ||
B、,(-
| ||
| C、(1,9) | ||
D、(-∞,-
|
 如图,一辆车要通过某十字路口,直行时前方刚好由绿灯转为红灯.该车前面已有4辆车依次在同一车道上排队等候(该车道只可以直行或左转行驶).已知每辆车直行的概率为
如图,一辆车要通过某十字路口,直行时前方刚好由绿灯转为红灯.该车前面已有4辆车依次在同一车道上排队等候(该车道只可以直行或左转行驶).已知每辆车直行的概率为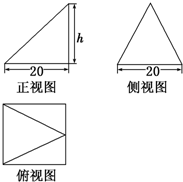 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是