Question

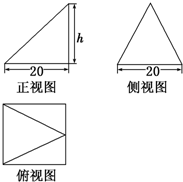已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是

8000

3

 cm³，则正视图中的h等于

 

cm．

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：由三视图可知，该几何体是一个四棱锥，且底面是一个边长为20的正方形，结合棱锥体积公式，可得答案．

解答： 解：由三视图可知，该几何体是一个四棱锥，
且底面是一个边长为20的正方形，
所以V=

1

3

×20×20×h=

8000

3

，
∴h=20．
故答案为：20．

点评：本题考查的知识点是由三视图求体积和表面积，由已知中的三视图分析出几何体的形状是解答的关键．