题目内容
设函数f（x）=(
)2x2-5x+b，g（x）=(
)x2+x+6，若f（x）＜g（x）对于任意实数x恒成立，则实数b的取值范围是（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、b＞12 | B、b＜12 |
| C、b＜15 | D、b＞15 |
考点：指、对数不等式的解法,指数函数的单调性与特殊点,不等关系与不等式
专题：不等式的解法及应用
分析：此题容易错选为B，错误原因是没有注意y=(
)x是单调减函数，根据单调性建立不等式，然后根据二次函数恒成立则判别式小于0，从而可求出b的取值范围．
| 1 |
| 2 |
解答：
解：∵f（x）＜g（x）即(
)2x2-5x+b＜(
)x2+x+6，
∴2x2-5x+b＞x2+x+6，
即x2-6x+b-6＞0恒成立，
则△=36-4（b-6）＜0，
解得b＞15．
故选：D．
| 1 |
| 2 |
| 1 |
| 2 |
∴2x2-5x+b＞x2+x+6，
即x2-6x+b-6＞0恒成立，
则△=36-4（b-6）＜0，
解得b＞15．
故选：D．
点评：本题主要考查了指数不等式的解法，以及恒成立问题，指数大小比较，当底数大于1时，指数越大，幂越大；当底数小于1大于0时，指数越小，幂越大当底数为负数时，要把负数提到外面，再比较大小．属于基础题．
练习册系列答案
期末100分闯关海淀考王系列答案
小学能力测试卷系列答案
相关题目
在区间（0，
）上随机取一个数x，则事件“sinx≥
”发生的概率为（ ）
| π |
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
，则这组数据的平均数等于圆(x-3)2+(y+
)2=1的圆心坐标是（ ）
| 7 |
| 3 |
A、(3，
| ||
B、(3，-
| ||
C、(-3，
| ||
D、(-
|
某校从高二年级学生中随机抽取40名学生，将他们的单元测试数学成绩（满分100分，成绩均为不低于40分的整数）分成六段：[40，50），[50，60），…[90，100]后得到如图所示的频率分布直方图．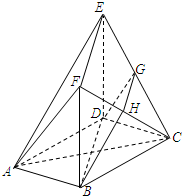
如图，在多面体ABCDEF中，底面ABCD是边长为2的正方形，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，G和H分别是CE和CF的中点．