题目内容
已知二次函数f(x)=mx2-2x-3,关于实数x的不等式f(x)≤0的解集为(-1,n)
(1)当a>0时,解关于x的不等式:ax2+n+1>(m+1)x+2ax;
(2)是否存在实数a∈(0,1),使得关于x的函数y=f(ax)-3ax+1(x∈[1,2])的最小值为-5?若存在,求实数a的值;若不存在,说明理由.
(1)当a>0时,解关于x的不等式:ax2+n+1>(m+1)x+2ax;
(2)是否存在实数a∈(0,1),使得关于x的函数y=f(ax)-3ax+1(x∈[1,2])的最小值为-5?若存在,求实数a的值;若不存在,说明理由.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)根据韦达定理得方程组求出m,n的值,再通过讨论a的范围,从而求出不等式的解集;
(2)把m=1代入方程,得出y=(ax)2-(3a+2)ax-3,令ax=t,(a2≤t≤a),则y=t2-(3a+2)t-3,得出函数的单调性,从而表示出y=f(t)的最小值,进而求出a的值.
(2)把m=1代入方程,得出y=(ax)2-(3a+2)ax-3,令ax=t,(a2≤t≤a),则y=t2-(3a+2)t-3,得出函数的单调性,从而表示出y=f(t)的最小值,进而求出a的值.
解答:
解:(1)由不等式mx2-2x-3≤0的解集为(-1,n)知
关于x的方程mx2-2x-3=0的两根为-1和n,且m>0
由根与系数关系,得
∴
,
所以原不等式化为(x-2)(ax-2)>0,
①当0<a<1时,原不等式化为(x-2)(x-
)>0,且2<
,解得x>
或x<2;
②当a=1时,原不等式化为(x-2)2>0,解得x∈R且x≠2;③
④当a>1时,原不等式化为(x-2)(x-
)>0,且2>
,解得x<
或x>2;
综上所述
当0<a≤1时,原不等式的解集为{x|x>
或x<2};
当1<a<2时,原不等式的解集为{x|x>2或x<
}.
(2)假设存在满足条件的实数a,
由(1)得:m=1,
∴f(x)=x2-2x-3,
∴y=f(ax)-3ax+1
=a2x-2ax-3-3ax+1
=(ax)2-(3a+2)ax-3,
令ax=t,(a2≤t≤a),
则y=t2-(3a+2)t-3
∴对称轴为:t=
,
又0<a<1,
∴a2<a<1,1<
<
,
∴函数y=t2-(3a+2)t-3在[a2,a]递减,
∴t=a时,y最小为:y=-2a2-2a-3=-5,
解得:a=
,
关于x的方程mx2-2x-3=0的两根为-1和n,且m>0
由根与系数关系,得
|
|
所以原不等式化为(x-2)(ax-2)>0,
①当0<a<1时,原不等式化为(x-2)(x-
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
②当a=1时,原不等式化为(x-2)2>0,解得x∈R且x≠2;③
④当a>1时,原不等式化为(x-2)(x-
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
综上所述
当0<a≤1时,原不等式的解集为{x|x>
| 2 |
| a |
当1<a<2时,原不等式的解集为{x|x>2或x<
| 2 |
| a |
(2)假设存在满足条件的实数a,
由(1)得:m=1,
∴f(x)=x2-2x-3,
∴y=f(ax)-3ax+1
=a2x-2ax-3-3ax+1
=(ax)2-(3a+2)ax-3,
令ax=t,(a2≤t≤a),
则y=t2-(3a+2)t-3
∴对称轴为:t=
| 3a+2 |
| 2 |
又0<a<1,
∴a2<a<1,1<
| 3a+2 |
| 2 |
| 5 |
| 2 |
∴函数y=t2-(3a+2)t-3在[a2,a]递减,
∴t=a时,y最小为:y=-2a2-2a-3=-5,
解得:a=
| ||
| 2 |
点评:本题考查了二次函数的性质,指数函数的性质,考查不等式的解法,考查分类讨论思想,换元思想,是一道综合题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
若sinatana>0,且
<0,则角a是( )
| cosa |
| tana |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
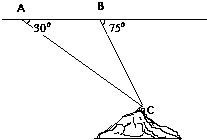 如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )
如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )