题目内容
不等式组
表示的平面区域的面积为 .
|
考点:简单线性规划,二元一次不等式(组)与平面区域
专题:数形结合,不等式的解法及应用
分析:由约束条件作出可行域,联立方程组求出三角形三点的坐标,直接由三角形的面积公式得答案.
解答:
解:由约束条件
作出可行域如图,

分别联立方程组
,
,
,可得
A(2,-2),B(2,6),C(-2,2).
∴平面区域的面积为S=
×8×4=16.
故答案为:16.
|

分别联立方程组
|
|
|
A(2,-2),B(2,6),C(-2,2).
∴平面区域的面积为S=
| 1 |
| 2 |
故答案为:16.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是基础题.

练习册系列答案
相关题目
若sinatana>0,且
<0,则角a是( )
| cosa |
| tana |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数f(x)=2x-1,x∈{-1,1},则f(x)的值域为( )
| A、[-3,1) |
| B、(-3,1] |
| C、[-3,1] |
| D、{-3,1} |
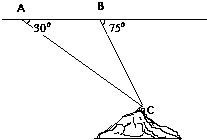 如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )
如图,飞机的航线和山顶在同一铅垂面内,若飞机的高度为海拔18km,速度为1000km/h,飞行员先看到山顶的俯角为30°,经过1min后又看到山顶的俯角为75°,则山顶的海拔高度为(精确到0.1)( )| A、11.4 | B、6.6 |
| C、6.5 | D、5.6 |
函数y=
的定义域是( )
| 1 |
| ln(x-2) |
| A、(-∞,2) |
| B、(2,+∞) |
| C、(2,3)∪(3,+∞) |
| D、(2,4)∪(4,+∞) |