题目内容
8.若四面体ABCD的三组对棱分别相等,即AB=CD,AC=BD,AD=BC,给出下列结论:
①四面体ABCD每个面的面积相等;
②从四面体ABCD每个顶点出发的三条棱两两夹角之和大于90° 而小于180°;
③连结四面体ABCD每组对棱中点的线段相互垂直平分;
④从四面体ABCD每个顶点出发的三条棱的长可作为一个三角形的三边长;
其中正确结论的序号是①③④.(写出所有正确结论的序号)
分析 由条件可知四面体的棱为长方体的面对角线,根据长方体的性质判断各结论是否正确.
解答 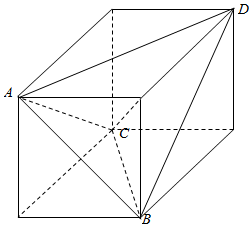 解:由条件可知四面体ABCD的四个面全等,故而①正确;
解:由条件可知四面体ABCD的四个面全等,故而①正确;
由条件可知四面体ABCD为长方体的面对角线组成的三棱锥,如图所示:
当长方体为正方体时,三棱锥任意一个顶点处的三个角均为60°,
故而从四面体ABCD每个顶点出发的三条棱两两夹角之和都是180°,故②错误;
由长方体的性质可知连结四面体ABCD每组对棱中点的线段为长方体对面的中心连线,故而③正确;
∵AC=BD,AB=CD,AD=BC,
∴过四面体任意一点的三条棱的长为△ABD的三边长,故而④正确.
故答案为:①③④.
点评 本题考查了棱锥的结构特征,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.设 a=1.10.9,b=0.91.1,c=0.90.9,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
19.抛物线y=(x-1)2的对称轴是( )
| A. | 0 | B. | 1 | C. | x=0 | D. | x=1 |
3.在△ABC中,BC=2,B=60°,若△ABC的面积等于$\frac{\sqrt{3}}{2}$,则AC边长为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 5 | D. | $\sqrt{5}$ |
13.若f(x)=$\left\{\begin{array}{l}f(x-5),x>0\\{2^x}+\int_0^{\frac{π}{6}}{cos3tdt,x≤0}\end{array}\right.$,则f(2017)=( )
| A. | $\frac{1}{24}$ | B. | $\frac{11}{24}$ | C. | $\frac{5}{24}$ | D. | $\frac{1}{2}$ |