题目内容

3．求证：sinA+sinB-cosAsin（A+B）=2sinAsin2$\frac{A+B}{2}$．

分析 由和差角的三角函数公式和二倍角公式，由左边向右边变形可得．

解答 证明：左边=sinA+sinB-cosAsin（A+B）
=sinA+sin[（A+B）-A]-cosAsin（A+B）
=sinA+sin（A+B）cosA-cos（A+B）sinA-cosAsin（A+B）
=sinA-cos（A+B）sinA=sinA[1-cos（A+B）]
=sinA（1-1+2sin2$\frac{A+B}{2}$）=2sinAsin2$\frac{A+B}{2}$=右边．

点评 本题考查三角函数恒等式的证明，涉及和差角的三角函数公式和二倍角公式，属中档题．

练习册系列答案
相关题目
13．若二项式（x+$\frac{1}{\sqrt{x}}$）6的展开式中的x3项大于15，且x为等比数列an的公比，则$\underset{lim}{n→∞}\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{{a}_{3}+{a}_{4}+…+{a}_{n}}$=1．
14．已知函数f（x）=ax3+$\frac{1}{2}$x2在x=1处的切线方程为4x-2y-5=0，记g（x）=$\frac{1}{f′（x）}$，程序框图如图所示，若输出的结果S＞$\frac{2011}{2012}$，则判断框中可以填入的关于n的判断条件是（　　）
A．n≤2011？B．n＞2011？C．n≤2012？D．n＞2012？
11．（1-x）（1+x）4的展开式中x3系数为-2．
18．已知命题p：方程$\frac{{x}^{2}}{m}$-$\frac{{y}^{2}}{m+3}$=1表示的曲线为双曲线；q：函数y=（m2-m-1）x为增函数，分别求出符合下列条件的实数m的范围．
（Ⅰ）若命题“p且q”为真；
（Ⅱ）若命题“p或q”为真，“p且q”为假．
8．已知函数f（x）=x2+4x+4，若存在实数t，当x∈[1，t]时，f（x+a）≤4x恒成立，则实数t的最大值为（　　）
A．4B．7C．8D．9
15．程序框图如图，该程序运行后，为使输出的y≤256，则循环体的判断框内①处应填（　　）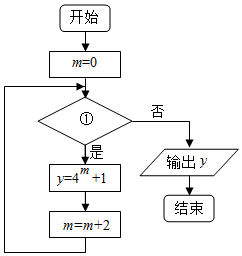
A．m＜2？B．m≤2？C．m≤3？D．m≤4？
12．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F（1，0），过点F的直线l交椭圆C于M，N两点，圆x2+y2=$\frac{2}{3}$与椭圆C的四个顶点构成的四边形相切．
（1）求椭圆C的方程；
（2）证明：$\frac{1}{|MF|}$+$\frac{1}{|NF|}$为定值，并求出此定值．
4．已知直线l1、l2与曲线W：mx2+ny2=1（m＞0，n＞0）分别相交于点A、B和C、D，我们将四边形ABCD称为曲线W的内接四边形．
（1）若直线l1：y=x+a和l2：y=x+b将单位圆W：x2+y2=1分成长度相等的四段弧，求a2+b2的值；
（2）若直线${l_1}：y=2x-\sqrt{10}，{l_2}：y=2x+\sqrt{10}$与圆W：x2+y2=4分别交于点A、B和C、D，求证：四边形ABCD为正方形；
（3）求证：椭圆$W：\frac{x^2}{2}+{y^2}=1$的内接正方形有且只有一个，并求该内接正方形的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网