题目内容
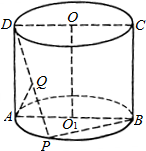 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在 |
| AB |
 |
| AP |
| 1 |
| 3 |
 |
| APB |
(Ⅰ)求证:AQ⊥PB;
(Ⅱ)若直线PD与面ABCD所成的角为30°,求圆柱OO1的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连接PA,证明PA⊥PB,PB⊥AD,推出PB⊥平面PAD 利用直线与平面垂直的性质定理证明AQ⊥PB.
(Ⅱ)过点P作PE⊥AB,E为垂足,连结CE,说明∠PDE就是直线PD与面ABCD所成的角,利用已知条件求出O1E=1,PE=
,然后求出AD,得到柱体的高,然后求解几何体的体积.
(Ⅱ)过点P作PE⊥AB,E为垂足,连结CE,说明∠PDE就是直线PD与面ABCD所成的角,利用已知条件求出O1E=1,PE=
| 3 |
解答:
(Ⅰ)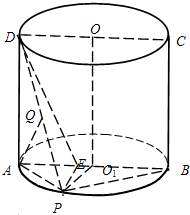 证明:连接PA,
证明:连接PA,
∵AB为底面的直径,
∴PA⊥PB,
又∵AD⊥面PAB,PB?平面PAB,
∴PB⊥AD.
又PA∩AB=A.
∴PB⊥平面PAD,
又AQ?平面PAD,
∴AQ⊥PB.
(Ⅱ)解:过点P作PE⊥AB,E为垂足,连结DE,
∵OO1⊥平面PAB,
∴平面ABCD⊥平面PAB,
∴PE⊥平面ABCD,
∴∠PDE就是直线PD与面ABCD所成的角,
∴∠PDE=30°,
又∵
=
,
∴O1E=1,PE=
,
又∵tan∠PDE=
,
∴DE=3,AD=
=
=2
,
∴V=Sh=π×22×2
=8
π.
 证明:连接PA,
证明:连接PA,∵AB为底面的直径,
∴PA⊥PB,
又∵AD⊥面PAB,PB?平面PAB,
∴PB⊥AD.
又PA∩AB=A.
∴PB⊥平面PAD,
又AQ?平面PAD,
∴AQ⊥PB.
(Ⅱ)解:过点P作PE⊥AB,E为垂足,连结DE,
∵OO1⊥平面PAB,
∴平面ABCD⊥平面PAB,
∴PE⊥平面ABCD,
∴∠PDE就是直线PD与面ABCD所成的角,
∴∠PDE=30°,
又∵
 |
| AP |
| 1 |
| 3 |
 |
| APB |
∴O1E=1,PE=
| 3 |
又∵tan∠PDE=
| PE |
| DE |
∴DE=3,AD=
| DE2-AE2 |
| 32-(2-1)2 |
| 2 |
∴V=Sh=π×22×2
| 2 |
| 2 |
点评:本题考查几何体的体积以及直线与平面所成角的求法,直线与平面平行的性质定理的应用,考查空间想象能力以及计算能力.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 用两种不同的颜色给图中三个矩形随机涂色,每个矩形只涂一种颜色,则相邻两个矩形涂不同颜色的概率是
用两种不同的颜色给图中三个矩形随机涂色,每个矩形只涂一种颜色,则相邻两个矩形涂不同颜色的概率是