题目内容
在极坐标系下,直线ρcosθ=1与圆ρ=2cosθ相交的弦长为 .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:化直线和圆的极坐标方程为直角坐标方程,联立方程组求得直线和圆的两个交点的坐标,然后由两点间的距离公式得答案.
解答:
解:由ρcosθ=1,得x=1;
由ρ=2cosθ,得ρ2=2ρcosθ,即x2+y2-2x=0,
联立
,解得
或
.
∴直线x=1与圆x2+y2-2x=0相交所得弦长为|y2-y1|=2.
故答案为:2.
由ρ=2cosθ,得ρ2=2ρcosθ,即x2+y2-2x=0,
联立
|
|
|
∴直线x=1与圆x2+y2-2x=0相交所得弦长为|y2-y1|=2.
故答案为:2.
点评:本题考查了极坐标方程化直角坐标方程,考查了直线与圆的关系,是基础的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=log4x-|x-4|的零点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
 阅读右边程序框图,为使输出的数据为30,则判断框中应填入的条件为( )
阅读右边程序框图,为使输出的数据为30,则判断框中应填入的条件为( )| A、i≤4 | B、i≤5′ |
| C、i≤6 | D、i≤7 |
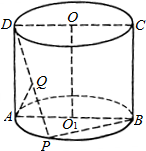 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在
