题目内容
已知函数f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(1-x),若数列{an}满a1=
,且an+1=
,则f(a11)=( )
| 1 |
| 2 |
| 1 |
| 1-an |
| A、6 | B、-6 | C、2 | D、-2 |
考点:数列递推式
专题:函数的性质及应用,点列、递归数列与数学归纳法
分析:由已知求出函数在x>0时的解析式,再由数列递推式求出a11,代入函数解析式得答案.
解答:
解:设x>0,则-x<0,
∵f(x)是定义在R上的奇函数,
∴f(x)=-f(-x)=-[-x(1+x)]=x(1+x).
由a1=
,且an+1=
,的a2=
=
=2,
a3=
=
=-1,a4=
=
=
.
…
∴数列{an}是以3为周期的周期数列,
则a11=a3×3+2=a2=2.
∴f(a11)=f(2)=2×(2+1)=6.
故选:A.
∵f(x)是定义在R上的奇函数,
∴f(x)=-f(-x)=-[-x(1+x)]=x(1+x).
由a1=
| 1 |
| 2 |
| 1 |
| 1-an |
| 1 |
| 1-a1 |
| 1 | ||
1-
|
a3=
| 1 |
| 1-a2 |
| 1 |
| 1-2 |
| 1 |
| 1-a3 |
| 1 |
| 1-(-1) |
| 1 |
| 2 |
…
∴数列{an}是以3为周期的周期数列,
则a11=a3×3+2=a2=2.
∴f(a11)=f(2)=2×(2+1)=6.
故选:A.
点评:本题考查了数列递推式,考查了数列的周期性,训练了函数解析式的求法,是中档题.

练习册系列答案
相关题目
设F为双曲线
-
=1(a>0,b>0)的右焦点,若双曲线与渐近线在第一象限分别存在点PQ.使得P为QF的中点,则双曲线离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) | ||
| B、(2,+∞ | ||
C、(1,
| ||
D、(
|
 某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为
某商场根据甲、乙两种不同品牌的洗衣粉在周一至周五每天的销量绘成如图所示的茎叶图,若两种品牌销量的平均数为. |
| x甲 |
. |
| x乙 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
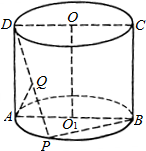 如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在
如图,圆柱OO1的底面圆半径为2,ABCD为经过圆柱轴OO1的截面,点P在