题目内容
已知f(x)=2xlnx,g(x)=-x2+ax-3,对一切x∈(0,+∞),f(x)≥g(x)恒成立,则实数a的取值范围是( )
| A、(-∞,4] |
| B、(-∞,5] |
| C、[6,+∞) |
| D、[4,+∞) |
考点:导数在最大值、最小值问题中的应用
专题:计算题,不等式的解法及应用
分析:f(x)≥g(x)可整理为a≤2lnx+x+
,令h(x)=2lnx+x+
(x>0),则问题转化为h(x)min≥a,利用导数易求h(x)min.
| 3 |
| x |
| 3 |
| x |
解答:
解:f(x)≥g(x)即2xlnx≥-x2+ax-3,
整理得a≤2lnx+x+
,
令h(x)=2lnx+x+
(x>0),
则h′(x)=
+1-
=
,
当0<x<1时,h′(x)<0,h(x)递减;当x>1时,h′(x)>0,h(x)递增,
∴h(x)min=h(1)=4,
∵f(x)≥g(x)恒成立,∴a≤4,
故选A.
整理得a≤2lnx+x+
| 3 |
| x |
令h(x)=2lnx+x+
| 3 |
| x |
则h′(x)=
| 2 |
| x |
| 3 |
| x2 |
| (x+3)(x-1) |
| x2 |
当0<x<1时,h′(x)<0,h(x)递减;当x>1时,h′(x)>0,h(x)递增,
∴h(x)min=h(1)=4,
∵f(x)≥g(x)恒成立,∴a≤4,
故选A.
点评:该题考查函数恒成立问题,考查利用导数研究函数的最值,考查转化思想,考查学生分析解决问题的能力.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
下列函数中增加得最快的是( )
| A、y=2x |
| B、y=3x |
| C、y=4x |
| D、y=ex |
下列说法正确的是( )
| A、小于90°的角是锐角 |
| B、大于90°的角是钝角 |
| C、0°~90°间的角一定是锐角 |
| D、锐角一定是第一象限的角 |
根据下列情况,判断三角形解的情况,其中正确的是( )
| A、a=8,b=16,A=30°,有两解 |
| B、b=18,c=20,B=60°,有一解 |
| C、a=5,c=2,A=90°,无解 |
| D、a=30,b=25,A=150°,有一解 |
一个算法的程序框图如图,则其输出结果是( )
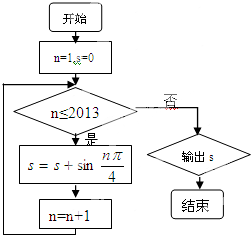

| A、0 | ||||
B、
| ||||
C、
| ||||
D、
|
已知F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,O为原点,A为右顶点,P为双曲线左支上的任意一点,若
存在最小值为12a,则双曲线离心率e的取值范围是 ( )
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1|-|OA| |
| A、[5,+∞) |
| B、(2,5] |
| C、(1,5] |
| D、(1,2) |