题目内容
7．等比数列{an}中，S2=2，S4=8，则S6=（ ）| A． | -32 | B． | 32 | C． | -26 | D． | 26 |
分析 由等比数列的性质可得S2，S4-S2，S6-S4成等比数列，由题意可得关于S6的方程，解方程可得．
解答 解：由等比数列的性质可得S2，S4-S2，S6-S4成等比数列，
∴（S4-S2）2=S2（S6-S4），即（8-2）2=2（S6-8），
解关于S6的方程可得S6=26，
故选：D．
点评 本题考查等比数列的通项公式和等比数列的性质，属基础题．
练习册系列答案
相关题目
15．若直线l1：ax+2y+6=0与直线l2：x+（a-1）y-1=0垂直，则实数a=（ ）
| A． | $\frac{2}{3}$ | B． | -1 | C． | 2 | D． | -1或2 |
12．已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1，直线l与椭圆交于与椭圆相交于A、B两点，点P（1，1）是线段AB的中点，则直线l的斜率为（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |
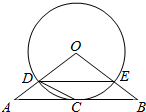如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC=CB．