题目内容
6．已知i是虚数单位，m是实数，z=（m2-5m+6）+（m-2）i，当m为何值时，z是（1）实数 （2）虚数 （3）纯虚数．
分析 （1）直接由虚部为0求得m值；
（2）由虚部不为0得答案；
（3）由实部为0且虚部不为0列式求得m值．
解答 解：（1）若z是实数，则m-2=0，即m=2；
（2）若z是虚数，则m-2≠0，即m≠2；
（3）若z是纯虚数，则$\left\{\begin{array}{l}{{m}^{2}-5m+6=0}\\{m-2≠0}\end{array}\right.$，解得m=3．
点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
17．已知集合A={x|x＜1}，B={x|3x＜1}，则（ ）
| A． | A∩B={x|x＜0} | B． | A∪B=R | C． | A∪B={x|x＞1} | D． | A∩B=∅ |
11．
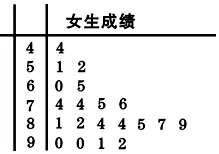为了研究某学科成绩（满分100分）是否与学生性别有关，采用分层抽样的方法，从高二年级抽取了30名男生和20名女生的该学科成绩，得到如图所示女生成绩的茎叶图．其中抽取的男生中有21人的成绩在80分以下，规定80分以上为优秀（含80分）．
（1）请根据题意，将2×2列联表补充完整；
（2）据此列联表判断，是否有90%的把握认为该学科成绩与性别有关？
附：x2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
为了研究某学科成绩（满分100分）是否与学生性别有关，采用分层抽样的方法，从高二年级抽取了30名男生和20名女生的该学科成绩，得到如图所示女生成绩的茎叶图．其中抽取的男生中有21人的成绩在80分以下，规定80分以上为优秀（含80分）．（1）请根据题意，将2×2列联表补充完整；
| 优秀 | 非优秀 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
附：x2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
| 参考数据 | 当x2≤2.706时，无充分证据判定变量A，B有关联，可以认为两变量无关联； |
| 当x2＞2.706时，有90%的把握判定变量A，B有关联； | |
| 当x2＞3.841时，有95%的把握判定变量A，B有关联； | |
| 当x2＞6.635时，有99%的把握判定变量A，B有关联． |
18．已知复数z满足z（1+i）=2i，则z的共轭复数$\overline{z}$等于（ ）
| A． | 1+i | B． | 1-i | C． | -1+i | D． | -1-i |
16．函数f（x）=sin（2x+$\frac{π}{3}$）的最小正周期为（ ）
| A． | 4π | B． | 2π | C． | π | D． | $\frac{π}{2}$ |