题目内容
已知α∈(π,
),tanα=
,则sinα的值为( )
| 3π |
| 2 |
| 1 |
| 3 |
A、
| ||||
B、-
| ||||
C、±
| ||||
D、-
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:由条件利用同角三角函数的基本关系、以及三角函数在各个象限中的符号,求得sinα的值.
解答:
解:∵α∈(π,
),∴sinα<0,cosα<0,
又 tanα=
=
,sin2α+cos2α=1,则sinα=-
,
故选:D.
| 3π |
| 2 |
又 tanα=
| sinα |
| cosα |
| 1 |
| 3 |
| ||
| 10 |
故选:D.
点评:本题主要考查同角三角函数的基本关系的应用,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
i是虚数单位,复数(1-i)2的虚部为( )
| A、-2 | B、2 | C、-2i | D、2i |
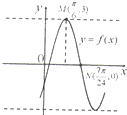 如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
如图,函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<