题目内容
y=x3在点M（-2，-8）处的切线方程是（ ）
| A、12x-y-16=0 |
| B、12x-y+16=0 |
| C、12x+y-16=0 |
| D、12x+y+16=0 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求导数，把x=-2代入求出切线的斜率，再代入直线的点斜式方程并化为一般式．
解答：
解：由题意得y′=3x2，
∴在点（-2，-8）处切线的斜率是k=12，
∴在点（-2，-8）处切线的方程是：y+8=12（x+2），
即12x-y+16=0，
故选：B．
∴在点（-2，-8）处切线的斜率是k=12，
∴在点（-2，-8）处切线的方程是：y+8=12（x+2），
即12x-y+16=0，
故选：B．
点评：本题考查了导数的几何意义，即在某点处的切线的斜率是该点处的导数值，以及直线方程的一般式和点斜式的应用．
练习册系列答案
相关题目
将一枚骰子抛掷两次，若先后出现的点数分别为x、y，则满足x=2y的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
计算sin46°cos16°+sin44°cos106°的结果等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合A={x|y=
}，集合B={y|y=x2，x∈R}，则A∪B=（ ）
| x+1 |
| A、ϕ |
| B、[0，+∞） |
| C、[1，+∞） |
| D、[-1，+∞） |
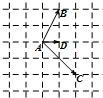已知向量| AC |
| AD |
| AB |
| AC |
| AB |
| AD |
| A、2 | B、-2 | C、3 | D、-3 |
已知全集U={1，2，3，4，5，6，7}，A={1，3，5，7}，则∁UA=（ ）
| A、{1，3，5，7} |
| B、∅ |
| C、{1，2，3，4，5，6，7} |
| D、{2，4，6} |
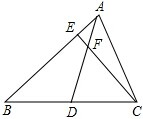如图，已知△ABC中，AE：EB=1：3，BD：DC=2：1，AD与CE相交于点F，则| EF |
| FC |
| AF |
| FD |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
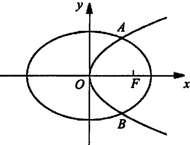如图，已知椭圆C1：