题目内容
16.已知正项数列{an} 中,$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$=$\frac{n(n+1)}{2}$(n∈N*),则数列{an}的通项公式为( )| A. | an=n | B. | an=n2 | C. | an=$\frac{n}{2}$ | D. | an=$\frac{{n}^{2}}{2}$ |
分析 根据已知可得$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n-1}}$=$\frac{n(n-1)}{2}$,与已知式子相减即可得出an.
解答 解:∵$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$=$\frac{n(n+1)}{2}$,
∴$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n-1}}$=$\frac{n(n-1)}{2}$(n≥2),
两式相减得$\sqrt{{a}_{n}}$=$\frac{n(n+1)}{2}$-$\frac{n(n-1)}{2}$=n,
∴an=n2,(n≥2)
又当n=1时,$\sqrt{{a}_{1}}$=$\frac{1×2}{2}=1$,
∴an=n2.n∈N*.
故选B.
点评 本题考查了数列通项公式的求法,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
11.一个几何体的三视图如图所示,则这个几何体的体积是( )
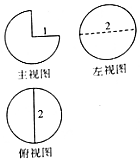

| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | π |
1.某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为20人)进行教学(两班的学生学习)(两班的学生学习数学勤奋程度和自觉性都一样).如图所示茎叶图如.
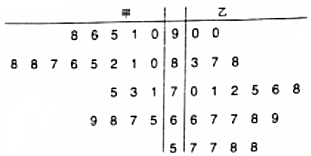
(1)现从乙班数学成绩不低于80分的同学中随机抽取两名同学,求至少有一名成绩为90分的同学被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2表,并判断有多大把握认为“成绩优秀与教学方式有关”.
附参考公式及数据:
(K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$)

(1)现从乙班数学成绩不低于80分的同学中随机抽取两名同学,求至少有一名成绩为90分的同学被抽中的概率;
(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2表,并判断有多大把握认为“成绩优秀与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | 14 | 8 | 22 |
| 不优秀 | 6 | 12 | 18 |
| 合计 | 20 | 20 | 40 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.79 | 10.828 |
8.已知F1(0,-1),F2(0,1)是椭圆的两个焦点,过F1的直线l交椭圆于M,N两点,若△MF2N的周长为8,则椭圆方程为( )
| A. | $\frac{{y}^{2}}{16}$+$\frac{{x}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |