题目内容
6.若直线ax+by=1(a,b都是正实数)与圆x2+y2=1相交于A,B两点,当△AOB(O是坐标原点)的面积最大时,a+b的最大值为2.分析 当△AOB面积取最大值时,OA⊥OB,圆心O(0,0)到直线直线l的距离为$\frac{\sqrt{2}}{2}$,由此利用基本不等式,能求出a+b的最大值.
解答 解:当△AOB面积取最大值时,OA⊥OB,则圆心到直线的距离d=$\frac{1}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{\sqrt{2}}{2}$,
∴a2+b2=2,
∴(a+b)2≤2(a2+b2)=4,∴a+b≤2,
∴a+b的最大值为2,
故答案为2.
点评 本题主要考查了直线与圆的位置关系,属于中档试题,本题的解答当△AOB面积取最大值时,OA⊥OB,此时圆心O到直线的距离为$\frac{\sqrt{2}}{2}$是解答本题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
16.已知倾斜角为α的直线l与直线x+2y-4=0垂直,则$cos(\frac{2017}{2}π-2α)$的值为( )
| A. | 2 | B. | $-\frac{1}{2}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
1.已知tanα=2,则sin2α+sinαcosα的值为( )
| A. | $\frac{6}{5}$ | B. | 1 | C. | $\frac{4}{5}$ | D. | $\frac{2}{3}$ |
11.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,点M,N为长轴的两个端点,若在椭圆上存在点H,使${k_{MH}}{k_{NH}}∈(-\frac{1}{2},0)$,则离心率e的取值范围为( )
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
16.已知正项数列{an} 中,$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$=$\frac{n(n+1)}{2}$(n∈N*),则数列{an}的通项公式为( )
| A. | an=n | B. | an=n2 | C. | an=$\frac{n}{2}$ | D. | an=$\frac{{n}^{2}}{2}$ |

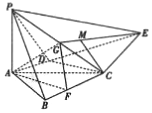 在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.
在四棱锥P-ABCE中,PA⊥底面ABCE,CD⊥AE,AC平分∠BAD,G为PC的中点,PA=AD=2,BC=DE,AB=3,CD=2$\sqrt{3}$,F,M分别为BC,EG上一点,且AF∥CD.