题目内容
8．已知F1（0，-1），F2（0，1）是椭圆的两个焦点，过F1的直线l交椭圆于M，N两点，若△MF2N的周长为8，则椭圆方程为（ ）| A． | $\frac{{y}^{2}}{16}$+$\frac{{x}^{2}}{15}$=1 | B． | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | C． | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D． | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
分析 由题意可设椭圆的标准方程为：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）．△MF2N的周长为8，可得4a=8，又c=1，a2=b2+c2，联立解出即可得出．
解答 解：由题意可设椭圆的标准方程为：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）．
∵△MF2N的周长为8，∴4a=8，又c=1，a2=b2+c2，
解得a=2，b2=3．
可得椭圆的标准方程为：$\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1．
故选：D．
点评 本题考查了椭圆的定义标准方程及其性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
19．设a=cos50°cos127°+cos40°cos37°，b=$\frac{\sqrt{2}}{2}$（sin56°-cos56°），c=$\frac{1-ta{n}^{2}39°}{1+ta{n}^{2}39°}$，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | b＞a＞c | C． | c＞a＞b | D． | a＞c＞b |
16．已知正项数列{an} 中，$\sqrt{{a}_{1}}$+$\sqrt{{a}_{2}}$+…+$\sqrt{{a}_{n}}$=$\frac{n（n+1）}{2}$（n∈N*），则数列{an}的通项公式为（ ）
| A． | an=n | B． | an=n2 | C． | an=$\frac{n}{2}$ | D． | an=$\frac{{n}^{2}}{2}$ |
13．已知圆C的方程为x2+y2=1，直线l的方程为x+y=2，过圆C上任意一点P作与l夹角为45°的直线交l于A，则|PA|的最小值为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $\sqrt{2}-1$ | D． | $2-\sqrt{2}$ |
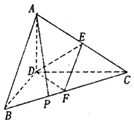已知三棱锥A-BCD，AD⊥平面BCD，BD⊥CD，AD=BD=2，CD=2$\sqrt{3}$，E，F分别是AC，BC的中点．