题目内容
15.如图所示,某空间几何体的正视图与侧视图相同,则此几何体的表面积为( )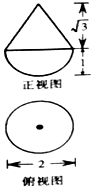
| A. | 6π | B. | $\frac{2π}{3}+\sqrt{3}$ | C. | 4π | D. | $2π+\sqrt{3}$ |
分析 几何体是半球上叠一个圆锥,球的半径等于圆锥底面圆半径R,R=1,圆锥母线长l=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}=2$,利用球、圆锥表面积公式计算即可.
解答 解:该几何体是半球上叠一个圆锥,球的半径等于圆锥底面圆半径R,R=1,
圆锥母线长l=$\sqrt{{1}^{2}+(\sqrt{3})^{2}}=2$
∴此几何体的表面积为$\frac{1}{2}×4π{R}^{2}+πRl=4π$.
故选:C
点评 本题考查了组合体的三视图,即圆锥、球的表面积,属于中档题.

练习册系列答案
相关题目
10.将二进制数10110(2)化为十进制数结果为( )
| A. | 19 | B. | 22 | C. | 44 | D. | 14 |
20.执行如图所示的程序图,则输出的S值为( )


| A. | 4 | B. | 3 | C. | -2 | D. | -3 |
7.“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是( )
| A. | 完全归纳推理 | B. | 归纳推理 | C. | 类比推理 | D. | 演绎推理 |
5.执行如图所示的程序框图,若输入p=2017,则输出i的值为( )
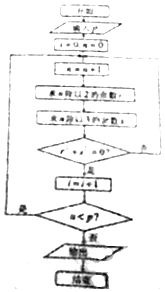

| A. | 335 | B. | 336 | C. | 337 | D. | 338 |