题目内容
16.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )
| A. | 32+8π | B. | 32+$\frac{8π}{3}$ | C. | 16+$\frac{8π}{3}$ | D. | 16+8π |
分析 该几何体正四棱柱上叠一个圆锥,圆锥的底面半径为2,高为2,正四棱柱的底面边长为2$\sqrt{2}$,高为4,利用体积公式计算即可.
解答 解:该几何体正四棱柱上叠一个圆锥,
圆锥的底面半径为2,高为2,故其体积为$\frac{1}{3}×π×{2}^{2}×2=\frac{8π}{3}$
正四棱柱的底面边长为2$\sqrt{2}$,高为4,其体积为2$\sqrt{2}$×$2\sqrt{2}$×4=32;
∴该几何体的体积为32+$\frac{8π}{3}$,
故选:B.
点评 本题考查了几何体的三视图,属于中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
7.“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是( )
| A. | 完全归纳推理 | B. | 归纳推理 | C. | 类比推理 | D. | 演绎推理 |
1.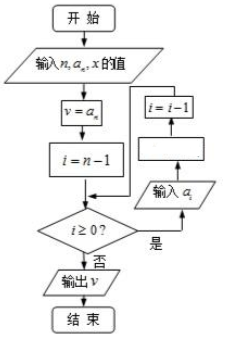 我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )
我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )
 我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )
我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出了计算多项式f(x)=anxn+an-1xn-1+…+a1x+a0的值的秦九韶算法,即将f(x)改写成如下形式:f(x)=(…((anx+an-1)x+an-2)x+…+a1)x+a0,首先计算最内层一次多项式的值,然后由内向外逐层计算一次多项式的值,这种算法至今仍是比较先进的算法,将秦九韶算法用程序框图表示如图,则在空白的执行框内应填入( )| A. | v=vx+ai | B. | v=v(x+ai) | C. | v=aix+v | D. | v=ai(x+v) |
8.已知f(x)=4x3-6x2+m(m为常数)在[-2,1]上有最大值5,那么此函数在[-2,1]上的最小值是( )
| A. | 3 | B. | -49 | C. | -52 | D. | -51 |
5.执行如图所示的程序框图,若输入p=2017,则输出i的值为( )
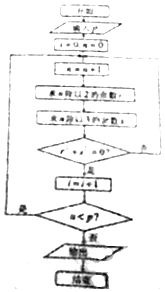

| A. | 335 | B. | 336 | C. | 337 | D. | 338 |