题目内容
2.若集合A={2,4,6,8},B={x|x2-9x+18≤0},则A∩B=( )| A. | {2,4} | B. | {4,6} | C. | {6,8} | D. | {2,8} |
分析 求出B中不等式的解集确定出B,找出A与B的交集即可.
解答 解:∵A={2,4,6,8},B={x|x2-9x+18≤0}={x|(x-3)(x-6)≤0}={x|3≤x≤6},
∴A∩B={4,6},
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
13.已知函数f(x)=$\frac{sin(4x+\frac{π}{3})}{sin(2x+\frac{2π}{3})}$ 的图象与g(x)的图象关于直线x=$\frac{π}{12}$ 对称,则g(x)的图象的一个对称中心为( )
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
14.已知集合M={x|lnx>0},N={x|x2-3x-4>0},则M∩N=( )
| A. | (-1,4) | B. | (1,+∞) | C. | (1,4) | D. | (4,+∞) |
17.若的(x2+a)(x-$\frac{1}{x}$)10展开式中x6的系数为-30,则常数a=( )
| A. | -4 | B. | -3 | C. | 2 | D. | 3 |
7.设函数f(x)=x2-2x-3,若从区间[-2,4]上任取一个实数x0,则所选取的实数x0满足f(x0)≤0的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
9.已知直线y=mx与x2+y2-4x+2=0相切,则m值为( )
| A. | ±$\sqrt{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±1 |
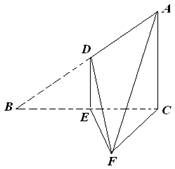 如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.
如图,直角△ABC中,∠ACB=90°,BC=2AC=4,D、E分别是AB、BC边的中点,沿DE将△BDE折起至△FDE,且∠CEF=60°.