题目内容
13.已知函数f(x)=$\frac{sin(4x+\frac{π}{3})}{sin(2x+\frac{2π}{3})}$ 的图象与g(x)的图象关于直线x=$\frac{π}{12}$ 对称,则g(x)的图象的一个对称中心为( )| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
分析 由已知利用函数的对称性可求g(x),进而利用余弦函数的图象和性质即可得解.
解答 解:∵函数f(x)=$\frac{sin(4x+\frac{π}{3})}{sin(2x+\frac{2π}{3})}$ 的图象与g(x)的图象关于直线x=$\frac{π}{12}$ 对称,
设P(x,y)为函数g(x)图象上的任意一点,
则P关于直线x=$\frac{π}{12}$的对称点P′($\frac{π}{6}$-x,y)在f(x)图象上,
∴满足y=f($\frac{π}{6}$-x)=$\frac{sin4x}{sin2x}$=2cos2x,可得:g(x)=2cos2x,
∴由2x=kπ+$\frac{π}{2}$,k∈Z,解得x=$\frac{kπ}{2}$+$\frac{π}{4}$,k∈Z,
∴当k=0时,则g(x)的图象的对称中心为($\frac{π}{4}$,0).
故选:C.
点评 本题主要考查了函数的对称性,余弦函数的图象和性质,考查了转化思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.袋中装有大小相同的四个球,四个球上分别标有数字“2”,“3”,“4”,“6”,现从中随机选取三个球,则所选的三个球上的数字能构成等差数列的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
18.已知函数f(x)=$\frac{sin(\frac{2π}{3}-4x)}{cos(2x+\frac{π}{6})}$的图象与g(x)的图象关于直线x=$\frac{π}{12}$对称,则g(x)的图象的一个对称中心为( )
| A. | ($\frac{π}{6}$,0) | B. | ($\frac{π}{3}$,0) | C. | ($\frac{π}{4}$,0) | D. | ($\frac{π}{2}$,0) |
2.若集合A={2,4,6,8},B={x|x2-9x+18≤0},则A∩B=( )
| A. | {2,4} | B. | {4,6} | C. | {6,8} | D. | {2,8} |
 ,
, ,则
,则 的值为 .
的值为 .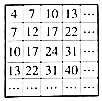 1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.
1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.