题目内容
14.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=2,$\overrightarrow{b}$=(4cosα,-4sinα),且$\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$),设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则θ等于$\frac{π}{3}$.分析 根据平面向量的数量积运算与夹角公式,即可求出$\overrightarrow{a}$、$\overrightarrow{b}$夹角的大小.
解答 解:∵|$\overrightarrow{a}$|=2,$\overrightarrow{b}$=(4cosα,-4sinα),
∴|$\overrightarrow{b}$|=$\sqrt{{(4cosα)}^{2}{+(-4sinα)}^{2}}$=4,
又$\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$),
∴$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}$•$\overrightarrow{b}$=22-$\overrightarrow{a}$•$\overrightarrow{b}$=0,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=4;
设$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为θ,则θ∈[0,π],
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|×|\overrightarrow{b}|}$=$\frac{4}{2×4}$=$\frac{1}{2}$,
∴θ=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查了平面向量数量积运算与夹角公式的应用问题,是基础题目.

 灵星计算小达人系列答案
灵星计算小达人系列答案| A. | {2,4} | B. | {4,6} | C. | {6,8} | D. | {2,8} |
| A. | $\frac{175}{32}$里 | B. | 1050 里 | C. | $\frac{22575}{32}$里 | D. | 2100里 |
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{7\sqrt{3}}{2}$ | D. | $\frac{8\sqrt{3}}{3}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | (0,2] | B. | [0,2) | C. | (2,3) | D. | [2,3) |
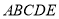 由直角梯形
由直角梯形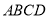 与直角△
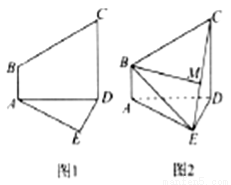
与直角△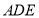 构成,如图1所示,
构成,如图1所示,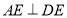 ,
,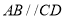 ,
,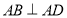 ,且
,且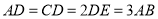 ,将梯形
,将梯形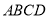 沿着
沿着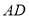 折起,形成如图2所示的几何体,且使平面
折起,形成如图2所示的几何体,且使平面
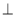 平面
平面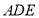 .
.
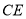 上存在点
上存在点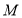 ,且
,且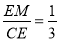 ,证明:
,证明: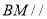 平面
平面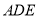 ;
;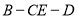 的平面角的余弦值.
的平面角的余弦值.