题目内容
9.已知直线y=mx与x2+y2-4x+2=0相切,则m值为( )| A. | ±$\sqrt{3}$ | B. | ±$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{3}}{2}$ | D. | ±1 |
分析 化圆的方程为标准方程,求得圆心与半径,利用圆心到直线的距离等于半径,即可求得m的值.
解答 解:圆x2+y2-4x+2=00的标准方程为(x-2)2+y2=2,
∴圆心(2,0),半径为$\sqrt{2}$
∵直线y=mx与x2+y2-4x+2=0相切,
∴$\frac{|2m|}{\sqrt{{m}^{2}+1}}$=$\sqrt{2}$
∴m=1或-1
故选:D.
点评 本题考查直线与圆的位置关系,利用圆心到直线的距离等于半径是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若集合A={2,4,6,8},B={x|x2-9x+18≤0},则A∩B=( )
| A. | {2,4} | B. | {4,6} | C. | {6,8} | D. | {2,8} |
19.已知$\overrightarrow{m}$,$\overrightarrow{n}$为两个非零向量,且|$\overrightarrow{m}$|=2,|$\overrightarrow{m}$+2$\overrightarrow{n}$|=2,则|$\overrightarrow{n}$|+|2$\overrightarrow{m}$+$\overrightarrow{n}$|的最大值为( )
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | $\frac{7\sqrt{3}}{2}$ | D. | $\frac{8\sqrt{3}}{3}$ |
14.已知函数f(x)=lnx+$\frac{ax}{x+1}$(a∈R).
(1)若函数f(x)在区间(1,4)上单调递增,求a的取值范围;
(2)若函数y=f(x)的图象与直线y=2x相切,求a的值.
(1)若函数f(x)在区间(1,4)上单调递增,求a的取值范围;
(2)若函数y=f(x)的图象与直线y=2x相切,求a的值.
1.设p:2x<1,q:x(x+1)<0,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
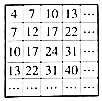 1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.
1934年,来自东印度(今孟加拉国)的学者森德拉姆发现了“正方形筛子”,其数字排列规律与等差数列有关,如图,则“正方形筛子”中,位于第8行第7列的数是127.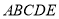 由直角梯形
由直角梯形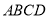 与直角△
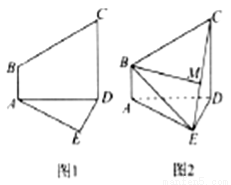
与直角△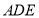 构成,如图1所示,
构成,如图1所示,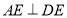 ,
,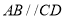 ,
,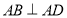 ,且
,且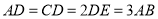 ,将梯形
,将梯形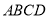 沿着
沿着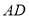 折起,形成如图2所示的几何体,且使平面
折起,形成如图2所示的几何体,且使平面
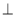 平面
平面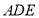 .
.
 上存在点
上存在点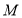 ,且
,且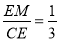 ,证明:
,证明: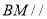 平面
平面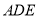 ;
;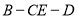 的平面角的余弦值.
的平面角的余弦值.