题目内容
7．设函数f（x）=x2-2x-3，若从区间[-2，4]上任取一个实数x0，则所选取的实数x0满足f（x0）≤0的概率为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
分析 由题意知本题是一个几何概型，概率的值为对应长度之比，根据题目中所给的不等式解出解集，解集在数轴上对应的线段的长度之比等于要求的概率．
解答 解：由题意知本题是一个几何概型，概率的值为对应长度之比，
由f（x0）≤0，得到x02-2x0-3≤0，且x0∈[-2，4]
解得：-1≤x0≤3，
∴P=$\frac{3+1}{4+2}$=$\frac{2}{3}$，
故选：A．
点评 本题主要考查了几何概型，以及一元二次不等式的解法，概率题目的考查中，概率只是一个载体，其他内容占的比重较大，属于基础题．
练习册系列答案
相关题目
18．已知函数f（x）=$\frac{sin（\frac{2π}{3}-4x）}{cos（2x+\frac{π}{6}）}$的图象与g（x）的图象关于直线x=$\frac{π}{12}$对称，则g（x）的图象的一个对称中心为（ ）
| A． | （$\frac{π}{6}$，0） | B． | （$\frac{π}{3}$，0） | C． | （$\frac{π}{4}$，0） | D． | （$\frac{π}{2}$，0） |
19．F1、F2是双曲线C的焦点，过F1且与双曲线实轴垂直的直线与双曲线相交于A、B，且△F2AB为正三角形，则双曲线的离心率e=（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | 2 | D． | $\sqrt{5}$ |
15．
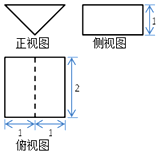《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”．某“堑堵”的三视图如图，则它的表面积为（ ）
《九章算术》中，将底面是直角三角形的直三棱柱称为“堑堵”．某“堑堵”的三视图如图，则它的表面积为（ ）| A． | 2 | B． | 4+2$\sqrt{2}$ | C． | 4+4$\sqrt{2}$ | D． | 6+4$\sqrt{2}$ |
2．若集合A={2，4，6，8}，B={x|x2-9x+18≤0}，则A∩B=（ ）
| A． | {2，4} | B． | {4，6} | C． | {6，8} | D． | {2，8} |
12．运行如图所示的程序框图，则输出的结果是（ ）
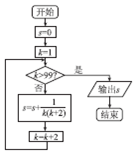
| A． | $\frac{49}{99}$ | B． | $\frac{50}{101}$ | C． | $\frac{51}{103}$ | D． | $\frac{1}{2}$ |
19．已知$\overrightarrow{m}$，$\overrightarrow{n}$为两个非零向量，且|$\overrightarrow{m}$|=2，|$\overrightarrow{m}$+2$\overrightarrow{n}$|=2，则|$\overrightarrow{n}$|+|2$\overrightarrow{m}$+$\overrightarrow{n}$|的最大值为（ ）
| A． | 4$\sqrt{2}$ | B． | 3$\sqrt{3}$ | C． | $\frac{7\sqrt{3}}{2}$ | D． | $\frac{8\sqrt{3}}{3}$ |
14．已知函数f（x）=lnx+$\frac{ax}{x+1}$（a∈R）．
（1）若函数f（x）在区间（1，4）上单调递增，求a的取值范围；
（2）若函数y=f（x）的图象与直线y=2x相切，求a的值．
（1）若函数f（x）在区间（1，4）上单调递增，求a的取值范围；
（2）若函数y=f（x）的图象与直线y=2x相切，求a的值．
14．已知双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），过左焦点F1作斜率为$\frac{\sqrt{3}}{3}$的直线交双曲线的右支于点P，且y轴平分线段F1P，则双曲线的离心率为（ ）
| A． | $\sqrt{3}$ | B． | $\sqrt{5}$+1 | C． | $\sqrt{2}$ | D． | 2+$\sqrt{3}$ |