题目内容
已知a>0,b>0,a+b=1,求
+
的最小值及此时a,b的值.
| 1 |
| 2a+1 |
| 2 |
| b+1 |
考点:函数的最值及其几何意义
专题:计算题,不等式的解法及应用
分析:先化简
+
=
+
,而由a+b=1得(2a+1)+(2b+2)=5;从而由基本不等式求最值.
| 1 |
| 2a+1 |
| 2 |
| b+1 |
| 1 |
| 2a+1 |
| 4 |
| 2b+2 |
解答:
解:∵
+
=
+
,
又∵a+b=1,∴(2a+1)+(2b+2)=5;
故
+
=
[(2a+1)+(2b+2)](
+
)
=
[5+
+
]
≥
(5+4)=
;
(当且仅当
=
,a=
,b=
时,等号成立);
故
+
的最小值为
,此时a=
,b=
.
| 1 |
| 2a+1 |
| 2 |
| b+1 |
| 1 |
| 2a+1 |
| 4 |
| 2b+2 |
又∵a+b=1,∴(2a+1)+(2b+2)=5;
故
| 1 |
| 2a+1 |
| 2 |
| b+1 |
| 1 |
| 5 |
| 1 |
| 2a+1 |
| 4 |
| 2b+2 |
=
| 1 |
| 5 |
| 4(2a+1) |
| 2b+2 |
| 2b+2 |
| 2a+1 |
≥
| 1 |
| 5 |
| 9 |
| 5 |
(当且仅当
| 4(2a+1) |
| 2b+2 |
| 2b+2 |
| 2a+1 |
| 1 |
| 3 |
| 2 |
| 3 |
故
| 1 |
| 2a+1 |
| 2 |
| b+1 |
| 9 |
| 5 |
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查了基本不等式在求最值中的应用,属于中档题.

练习册系列答案
相关题目
在平面直角坐标系xOy中,如果菱形OABC的边长为2,点B在y轴上,则菱形内(不含边界)的整点(横纵坐标都是整数的点)个数的取值集合是( )
| A、{1,3} |
| B、{0,1,3} |
| C、{0,1,3,4} |
| D、{0,1,2,3,4} |
 甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )
甲乙两同学在高二年级的6次数学测验成绩(满分100分)如图茎叶图所示,则下列说法正确的是( )| A、甲乙同学的平均成绩相同,但是甲同学的成绩比乙稳定 |
| B、甲乙同学的平均成绩相同,但是乙同学的成绩比甲稳定 |
| C、甲同学的平均成绩比乙同学好,但是乙同学的成绩比甲稳定 |
| D、乙同学的平均成绩比甲同学好,但是甲同学的成绩比乙稳定 |
已知l、m是不同的两条直线,α、β是不重合的两个平面,则下列命题中正确的是( )
| A、若l∥α,α⊥β,则l∥β |
| B、若l⊥α,α∥β,m?β,则l⊥m |
| C、若l⊥m,α∥β,m?β,则l⊥α |
| D、若l⊥α,α⊥β,则l∥β |
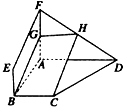 如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BE∥AF,BC∥AD,BC=
如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BE∥AF,BC∥AD,BC=