题目内容
8.圆x2+y2+ax-2ay+2a2+3a=0的圆心在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 根据圆的方程的一般式能够表示圆的充要条件,得到关于a的一元二次不等式,整理成最简单的形式,解一元二次不等式得到a的范围,即可得到结果.
解答 解:方程x2+y2+ax-2ay+2a2+3a=0表示圆,
∴a2+4a2-4(2a2+3a)>0,
∴3a2+12a<0,
∴-4<a<0,
∵圆心(-$\frac{a}{2}$,a),
∴圆心在第四象限.
故选:D.
点评 本题考查二元二次方程表示圆的条件,考查一元二次不等式的解法,是一个比较简单的题目.

练习册系列答案
相关题目
3.m<2是方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1表示双曲线的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.一个正三棱锥的外接球的半径为1,若球心在底面上,则该正三棱锥的体积是( )
| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{12}$ |
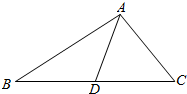 在△ABC中,D是BC中点,已知∠BAD+∠C=90°.
在△ABC中,D是BC中点,已知∠BAD+∠C=90°.