题目内容
19.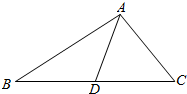 在△ABC中,D是BC中点,已知∠BAD+∠C=90°.
在△ABC中,D是BC中点,已知∠BAD+∠C=90°.(1)判断△ABC的形状;
(2)若△ADC的三边长是连续三个正整数,求∠BAC的余弦值.
分析 (1)设∠BAD=α,∠DAC=β,则由α+C=90°,可得β+B=90°,△ABD中,由正弦定理得:$\frac{sinB}{sinα}$=$\frac{AD}{BD}$,$\frac{sinC}{sinβ}$=$\frac{AD}{DC}$,结合BD=DC,可得sin2C=sin2B,结合范围B,C∈(0,π),即解得B=C或B+C=90°,从而得解.
(2)当B+C=90°时,$AD=\frac{1}{2}BC=DC$,与△ADC的三边长是连续三个正整数矛盾,
可得∠B=∠C,在直角三角形ADC中,设两直角边分别为n,n-1,斜边为n+1,由勾股定理得n=4,由余弦定理或二倍角公式即可求得cos∠BAC的值.
解答 解:(1)设∠BAD=α,∠DAC=β,
则由α+C=90°,∴β+B=90°,
△ABD中,由正弦定理得:$\frac{BD}{sinα}=\frac{AD}{sinB}$,即$\frac{sinB}{sinα}$=$\frac{AD}{BD}$,
同理得:$\frac{sinC}{sinβ}$=$\frac{AD}{DC}$,…(2分)
∵BD=DC,∴$\frac{sinB}{sinα}=\frac{sinC}{sinβ}$,∴sinαsinC=sinβsinB,
∵α+C=90°,β+B=90°,∴sinCcosC=sinBcosB,…(4分)
即sin2C=sin2B,因为B,C∈(0,π)
即B=C或B+C=90° …(6分)
∴△ABC是等腰三角形或直角三角形.…(7分)
(2)当B+C=90°时,$AD=\frac{1}{2}BC=DC$,与△ADC的三边长是连续三个正整数矛盾,
∴∠B=∠C,∴△ABC是等腰三角形.…(8分)
在直角三角形ADC中,设两直角边分别为n,n-1,斜边为n+1,由(n+1)2=n2+(n-1)2 得n=4,…(10分)
由余弦定理或二倍角公式得cos∠BAC=$\frac{7}{25}$ 或cos∠BAC=-$\frac{7}{25}$ (12分)
点评 本题主要考查了正弦定理,余弦定理,勾股定理,三角函数恒等变换的应用,考查了计算能力和转化思想,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | $\frac{{y}^{2}}{4}$+x2=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
| A. | f(-1)>f $({{{log}_{0.5}}\frac{1}{4}})$>f(lg0.5) | B. | f(lg0.5)>f(-1)>f $({{{log}_{0.5}}\frac{1}{4}})$ | ||
| C. | f $({{{log}_{0.5}}\frac{1}{4}})$>f(-1)>f(lg0.5) | D. | f(lg0.5)>f $({{{log}_{0.5}}\frac{1}{4}})$>f(-1) |
 如图,在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器,圆锥的上底圆周与鱼缸的底面正方形相切,圆锥的顶点在鱼缸的缸底上,现在向鱼缸内随机地投入一粒鱼食,则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是( )
如图,在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器,圆锥的上底圆周与鱼缸的底面正方形相切,圆锥的顶点在鱼缸的缸底上,现在向鱼缸内随机地投入一粒鱼食,则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是( )| A. | 1-$\frac{π}{4}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{12}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
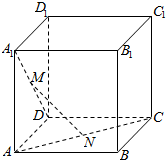 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.