题目内容
3.m<2是方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1表示双曲线的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合双曲线的方程进行判断即可.
解答 解:若方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1表示双曲线,
则(m-2)(6-m)<0,即(m-2)(m-6)>0,
解得m>6或m<2,
则m<2是方程$\frac{x^2}{m-2}+\frac{y^2}{6-m}$=1表示双曲线的充分不必要条件,
故选:A
点评 本题主要考查充分条件和必要条件的判断,利用双曲线的定义和性质求出m的范围是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.圆x2+y2+ax-2ay+2a2+3a=0的圆心在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.下列语句:
①{0}∈N;
②x2+y2=0;
③x2>x;
④{x|x2+1=0}.
其中是命题的个数是( )
①{0}∈N;
②x2+y2=0;
③x2>x;
④{x|x2+1=0}.
其中是命题的个数是( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
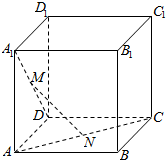 如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,M为A1D中点,N为AC中点. 在正方体ABCD-A1B1C1D1中,P、Q、R分别在棱AB、BB1、CC1上,且PD、QR相交于点O.求证:O、B、C三点共线.
在正方体ABCD-A1B1C1D1中,P、Q、R分别在棱AB、BB1、CC1上,且PD、QR相交于点O.求证:O、B、C三点共线.